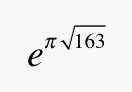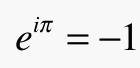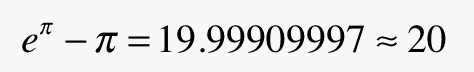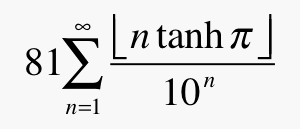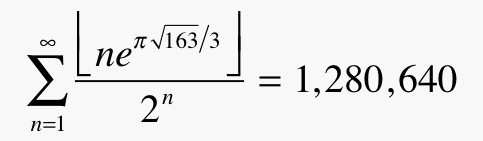2009 POSTS

JANUARY 2009

Should children learn math by starting with counting?

Two roads diverged in a yellow wood, And sorry I could not travel both, And be one traveler, long I stood, And looked down one as far as I could, To where it bent in the undergrowth;
Then took the other, as just as fair, And having perhaps the better claim, Because it was grassy and wanted wear; Though as for that, the passing there, Had worn them really about the same,
And both that morning equally lay, In leaves no step had trodden black, Oh, I kept the first for another day! Yet knowing how way leads on to way, I doubted if I should ever come back.
I shall be telling this with a sigh, Somewhere ages and ages hence: two roads diverged in a wood, and I — I took the one less traveled by, And that has made all the difference.
— Robert Frost, "Road Not Taken"

I began my last month’s column with the famous quotation by the German mathematician Leopold Kronecker (1823-1891): “God made the integers; all else is the work of man.” I ended the essay with a number of questions about the way we teach beginning students mathematics, and promised to say something about an alternative approach to the one prevalent in the US.

This month’s column begins where my last left off. To avoid repeating myself, I shall assume readers have read what I wrote last month. In particular, I provided evidence in support of my thesis (advanced by others in addition to myself) that, whereas numbers and perhaps other elements of basic, K-8 mathematics are abstracted from everyday experience, more advanced parts of the subject are created and learned as rule-specified, and often initially meaningless, “symbol games.” The former can be learned by the formation of a real-world-grounded chain of cognitive metaphors that at each stage provide an understanding of the new in terms of what is already familiar. The latter must be learned in much the same way we learn to play chess: first merely following the rules, with little comprehension, then, with practice, reaching a level of play where meaning and understanding emerge.

Lakoff and Nunez describe the former process in their book Where Mathematics Comes From. Most of us can recall that the latter was the way that we learned calculus—an observation that appears to run counter to—and which I think actually does refute—Lakoff and Nunez’s claim that the metaphor-construction process they describe yields all of pure mathematics.

If indeed there are these two, essentially different kinds of mathematical thinking, that must be (or at least are best) learned in very different ways, then a natural question is where, in the traditional K-university curriculum, the one ends and the other starts. And make no mistake about it, the two forms of learning I am talking about are very different. In the first, meaning gives rise to rules; in the second, rules eventually yield meaning. Somewhere between the acquisition of the (whole) number concept and calculus, the process of learning changes from one of abstraction to linguistic creation.

Note that both can generate mathematics that has meaning in the world and may be applied in the world. The difference is that in the former, the real-world connection precedes the new mathematics, in the latter the new mathematics must be “cognitively bootstrapped” before real-world connections can be understood and applications made.

Before I go any further, I should point out that, since I am talking about human cognition here, my simplistic classification into two categories is precisely that: a simplistic classification, convenient as a basis for making the general points I wish to convey. As always when people are concerned, the world is not black-and-white, but a continuous spectrum where there are many shades of gray between the two extremes. If my monthly email inbox is anything to go by, mathematicians, as a breed, seem particularly prone to trying to view everything in binary fashion. (So was I until I found myself, first a department chair and then a dean, when I had to deal with people and university politics on a daily basis!)

In particular, it may in principle be possible for a student, with guidance, to learn all of mathematics in the iterated-metaphor fashion described by Lakoff and Nunez, where each step is one of both understanding and competence (of performance). But in practice it would take far too long to reach most of contemporary mathematics. What makes it possible to learn advanced math fairly quickly is that the human brain is capable of learning to follow a given set of rules without understanding them, and apply them in an intelligent and useful fashion. Given sufficient practice, the brain eventually discovers (or creates) meaning in what began as a meaningless game, but it is in general not necessary to reach that stage in order to apply the rules effectively. An obvious example can be seen every year, when first-year university physics and engineering students learn and apply advanced methods of differential equations, say, without understanding them—a feat that takes the mathematics majors (where the goal very definitely is understanding) four years of struggle to achieve.

Backing up from university level now, where the approach of rapidly achieving procedural competence is effective for students who need to use various mathematical techniques, what is the best way to teach beginning mathematics to students in the early grades of the schools? Given the ability of young children to learn to play games, often highly complicated fantasy games, and the high level of skill they exhibit in videogames, many of which have a complexity level that taxes most adults—and if you don’t believe me, go ahead and try one for yourself (I have and they can be very hard to master)—I guess it might be possible they could learn elementary math that way. But I’m not aware that this approach has ever been tried, and it is not clear to me it would work. In fact, I suspect it would not. One thing we want our children to learn is how to apply mathematics to the everyday world, and that may well depend upon grounding the subject in that real world. After all, a university student who learns how to use differential equations in a rule-based fashion approaches the task with a more mature mind and an awful lot of prior knowledge and experience in using mathematics. In other words, the effectiveness of the rule-based, fast-track to procedural competence for older children and adults may well depend upon an initial grounding where the beginning math student abstracts the first basic concepts of (say) number and arithmetic from his or her everyday experience.

That, after all, is—as far as we know—how our ancestors first started out on the mathematical path many thousands of years ago. I caveated that last assertion with an “as far as we know” because, of course, all we have to go on is the archeological evidence of the artifacts they left behind. We don’t know how they actually thought about their world.

How it all began

We do know our ancestors began “counting” with various kinds of artifact (notches in sticks and bones, scratches on walls of caves, presumably piles of pebbles, etc.) at least 35,000 years ago, progressing to the more sophisticated clay tokens of the Sumerians around 8,000 years ago, to the emergence of abstract numbers (and written symbols to denote them) around 6,000 or 7,000 years ago. This development, which leads first to positive whole numbers with addition and eventually to positive rationals with addition was driven, we think, by commerce—the desire/need for peoples to keep track of their possessions and to trade with one another.

It is also clear from the archeological evidence that our early mathematically-capable forebears developed systems of measurement, both of length and of area, in order to measure land, plant crops, and eventually to design and erect buildings. From a present-day perspective, this looks awfully like the beginnings of the real number system, though just when that activity became numerical to an extent we would recognize today is not clear.

Today’s US mathematics curriculum starts with the positive whole numbers and addition, and builds on to in a fairly linear fashion, through negative numbers and rationals, until it reaches the real number system as the culmination. That approach can give rise to the assumption or even the belief that the natural numbers are somehow more basic or more natural than the reals. But that is not how things unfolded historically. True, if you try to build up the real numbers, starting with the natural numbers, you are faced with a long and complicated process that took mathematicians some two thousand years of effort to figure out, completing the task as recently as the end of the nineteenth century. But that does not mean that the real numbers are a cognitively more difficult concept to acquire than the natural numbers, or that one builds cognitively on the other. Humans have not only a natural ability to abstract discrete counting numbers from our everyday experience (sizes of collections of discrete objects) but also have a natural sense of continuous quantities such as length and volume (area seems less natural), and abstraction in that domain leads to positive real numbers.

In other words, from a cognitive viewpoint (as opposed to a mathematical one), the natural numbers are neither more fundamental nor more natural than the real numbers. They both arise directly from our experiences in the everyday world. Moreover, they appear to arise in parallel, out of different cognitive processes, used for different purposes, with neither dependent on the other. In fact, what little evidence there is from present-day brain research suggests that from a neurophysiological viewpoint, the real numbers—our sense of continuous number—is more basic than the natural numbers, which appear to build upon the continuous number sense by way of our language capacity. (See the recent books and articles of researchers such as Stanislaw Dehaene or Brian Butterworth for details.)

It seems then, that when we guide our children along the first steps of the long path to mathematical thinking, assuming we want to ground those key first steps in everyday experience and build upon natural human cognitive capacities, we have two possible ways to begin: the discrete world of assessing the sizes of collections and the continuous world of assessing lengths and volumes. The first leads to the natural numbers and counting, the second to the real numbers and measurement.

Two roads diverge in an educational thicket

If we start with measurement, the counting numbers and the positive rationals arise as special points on a continuous number line. Begin with counting and the real numbers arise by way of “filling in the gaps” in the rational number line. (In both cases you have to handle negative numbers as best you can when the need arises.) Neither approach seems on the face of it to offer significant advantages over the other from a learning perspective. Take your pick and live with the curricular consequences. (True, it is mathematically much harder to construct the real numbers from the natural numbers than to recognize the natural numbers and the rationals as special points on the real line, but the issue here is not one of formal mathematical construction but human cognition, building on everyday experience.)

In the Unites States and many other countries, the choice was made—perhaps unreflectively—long ago to take our facility for counting as the starting point, and thus to start the mathematical journey with the natural numbers. But there has been at least one serious attempt to build an entire mathematical curriculum on the other approach, and that is the focus of the remainder of this essay. Not because I think one is intrinsically better than the other – though that may be the case. Rather because, whichever approach we adopt, I think it is highly likely we will do a better job, and understand better what we are doing as teachers, if we are aware of an(y) alternative approach.

Indeed, knowledge of another approach may help us guide our students through particularly tricky areas such as the multiplication concept, the topic of some of my previous columns. As Piaget observed, and others have written on extensively, helping students achieve a good understanding of multiplication in the counting-first curriculum is extremely difficult. In a measuring-first curriculum, in contrast, some of the more thorny subtleties of multiplication that plague the counting-first progression simply do not arise. Maybe the way forward to greater success in early mathematics education is to adopt a hybrid approach that builds simultaneously on both human intuitions? (Arguably this occurs anyway to some extent. US children in a counting-first curriculum use lengths, volumes, and other real-number measures in their everyday lives, and children in the real-numbers-first curriculum I am about to describe can surely count, and possibly add and subtract natural numbers, before they get to school. But I am not aware of a formal school curriculum that tries to combine both approaches.)

Whichever of the two approaches we adopt, the expressed primary goal of current K-12 mathematics education is the same the world over: to equip future citizens with an understanding of, and procedural fluency with, the real number system. In the US school system, this is done progressively, with the first stages (natural numbers, integers, rationals) taught under the name “arithmetic” and the real numbers going under the banner “algebra”. (Until relatively recently, geometry and trigonometry were part of a typical school curriculum, bringing elements of the measuring-first approach into the classroom, but that was, as we all know, abandoned, though not without a fight by its proponents.)

It is interesting to note that coverage of the real numbers as “algebra” in the US approach ensures an entirely procedural treatment, avoiding the enormous difficulties involved in constructing the concept of real numbers starting from the rationals. Eventually, even our counting-first approach has to rely on our intuitions of, and everyday experience with, continuous measurement, even if it does not start with them.

Back in the USSR

And so to the one attempt I am aware of to build an entire contemporary curriculum that starts out not with counting but with measurement. It was developed in the Soviet Union during the second half of the twentieth century, and its leading proponent was the psychologist and educator Vasily Davydov (1930-1988). Davydov based his curriculum—nowadays generally referred to by his name, though others were involved in shaping it, most notably B. Elkonin—on the cognitive theories of the great Russian developmental psychologist Lev Semenovich Vygotsky (1896-1934).

In a series of studies of the development of primates, children, and traditional peoples, Vygotsky observed that cognitive development occurs when a problem is encountered for which previous methods of solution are inadequate (Vygotsky & Luria, 1993). The Davydov mathematics curriculum is built on top of this observation, and consists of a series of carefully sequenced problems that require progressively more powerful insights and methods for their solution. This is of course quite different from the instructional approach adopted by most US teachers, which consists of an instructional lecture, with worked examples, followed by a set of exercises focused on repeated practice of the particular skill the instructor has demonstrated in class.

But that is just the first of several differences between the two approaches. Whereas the US K-12 mathematics curriculum has an understanding of and computational facility with the real numbers system as the declared end-point, the first several years are taken up with the progression through positive whole numbers, fractions, and negative integers/rationals, with the real number system covered in the later grades, primarily under the name “algebra”. In contrast, the Davydov curriculum sets its sights squarely on the real number system from the getgo. Davydov believed that starting with specific numbers (the counting numbers) leads to difficulties later on when the students work with rational and real numbers or do algebra.

I’ll come back to the focus on the real number system momentarily, but first I need to introduce another distinquishing feature of Davydov’s approach.

Davydov took account of Vygotsky’s distinction between what he called spontaneous concepts and scientific concepts. The former arise when children abstract properties from everyday experiences or from specific instances; the latter develop from formal experiences with the properties themselves.

This distinction is more or less (but not entirely) the same as the one I discussed last month between mathematics we learn by abstraction from the world and mathematics we learn in a rule-based fashion the same way we learn to play chess. For example, children who learn about the positive integers by counting collections of objects thereby acquire a spontaneous concept. Learning to play chess leads to a “scientific” understanding of the game. The point I made earlier was that in my experience, both as a learner and a teacher of advanced mathematics, the scientific approach is the most efficient, and perhaps the only way, to learn a highly abstract subject such as calculus.

In last month’s column I asked where the abstract-it-from-the-world kind of mathematics (spontaneous concepts) ends and learn-it-by-the-rules kind (scientific concepts) starts. As I have noted, that question is a naive one that obscures the fact that there is most likely a continuous spectrum of change rather than a break point. A more usefully phrased question from an educational perspective is, which parts of mathematics should we teach in a spontaneous-concepts fashion and which in a scientific-concepts way?

The accepted wisdom in the US is that the spontaneous approach is the way to go at least all the way through K-8, and maybe all the way up to grade 12. (Adopting the approach all the way to grade 12 tends to force a presentation of calculus as “a method to calculate slopes”, which I personally dislike because it reduces one of the greatest ever achievements of human intellect to a bag of procedural tricks. But that is another issue for another time.)

The Davydov curriculum adopts the scientific-concepts approach from day 1. Davydov believed that learning mathematics using a general-to-specific, “scientific” approach leads to better mathematical understanding and performance in the long run than does the spontaneous approach. His reasoning was that if very young children begin their mathematics learning with abstractions, they will be better prepared to use formal abstractions in later school years, and their thinking will develop in a way that can support the capacity to handle more complex mathematics.

He wrote (Davydov 1966), “there is nothing about the intellectual capabilities of primary schoolchildren to hinder the algebraization of elementary mathematics. In fact, such an approach helps to bring and to increase these very capabilities children have for learning mathematics.”

I should stress that Davydov’s adoption of the “scientific-concepts” approach is not at all the same as teaching mathematics in an abstract, axiomatic fashion. (This is where my analogy with learning to play chess breaks down, as do all analogies sooner or later, no matter how helpful they may be at the start; which reminds me, did I ever mention the problems that can result from introducing multiplication as repeated addition?) The Davydov approach is grounded firmly in real-world experience, and lots of it. Indeed, students spend more time at the start doing nothing but real-world activities (before doing any explicit mathematics) than is the case in the US curriculum. But when the actual mathematical concepts are introduced, it is in a scientific fashion. The students are able to link the scientific concept to their real world experience not because that concept arose spontaneously out of that experience (it did not), but because they had been guided through sufficiently rich, preparatory real-world experiences that they are able to at once see how the concept applies to the real world. (In terms of metaphors, the metaphor mapping is contructed back from the new to the old, not the other way round as in the Lakoff and Nunez framework for learning.)

How the Russian rubber hits the road

Here is how Davydov’s curriculum starts (1975a). It begins by guiding the pupils through a series of exercises to develop an increasingly sophisticated, non-numerical understanding of size (length, volume, mass). Well, that is not entirely correct. The first, “pre-mathematical” step is to prepare the pupils for those exercises.

In Grade 1, the pupils are asked to describe and define physical attributes of objects that can be compared. As I hinted a moment ago, the intention is to provide a context for the children to explore relationships, both equality and comparative. Six-year-olds typically compare physically lengths, volumes, and masses of objects, and describe their findings with statements like H < B, where H and B are unspecified quantities being compared, not objects. (At this stage the unspecified quantities are not numbers.) Notice this immediate focus on abstractions. The physical context and the act of recording mean that the elements of “abstract” algebra are introduced in a meaningful way, and are not seen by the children as abstract.

For instance, the pupils are asked how to make unequal quantities equal or how to make equal quantities unequal by adding or subtracting an amount. Starting from a volume situation recorded as H < B, the children could achieve equality by adding to volume H or subtracting from volume B. They observe that whichever action they choose, the amount added or subtracted is the same. They are told it is called the difference.

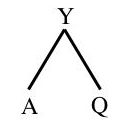
Only after they have mastered this pre-numeric understanding of size and of part-whole relationships are they presented with tasks that require quantification. For example, if they have been working with mass and have noticed that mass Y is the whole and masses A and Q are the parts that make up the whole, which they may be encouraged to express by means of a simple inverted-V diagram like this:

they can go on to write this in more formal ways:

Y = A + Q, Q + A = Y, Y – Q = A, Y – A = Q

This sets the stage for putting specific numerical values for the “variables” in order to solve equations that arise from real-world problems. (Numbers, that is, real numbers, are introduced in the second half of the first grade, as abstract measures of lengths, volumes, masses, and the like.) As a result, the pupils do not have to learn rules for solving algebraic equations; rather they become sophisticated in reasoning directly about part-whole relationships.

When the pupils get to multiplication and division, Davydov’s curriculum requires that they connect the new actions of multiplication and division with their prior knowledge of measurement and place value, as well as addition and subtraction, and to apply them to problems involving the metric system, number systems in other bases (studied in grade 1), area and perimeter, and the solution of more complex equations. In other words, the new operations come both with real world grounding and their connections to previously learned mathematics. Thee pupils have to explore the two new operations and their systemic interrelationships with previously learned concepts. They are constantly presented with problems that require them to forge connections to prior knowledge. Every new problem is different in some significant way from its predecessors and its successors. (Contrast this to the US approach where problems are presented in sets, with each set focusing on a single procedure.) As a result, the pupils must continuously think about what they are doing in order that it makes sense to them. By working through many problems designed so make them create connections between the new actions of multiplying and dividing and their previous knowledge of addition, subtraction, positional systems, and equations, they integrate their knowledge into a single conceptual system.

Thus, the Davydov curriculum is grounded in the real world, but the starting point is the continuous world of measurement rather than the discrete world of counting. I don’t know about you, but measurement and counting both seem to me to offer pretty concrete starting points for the mathematical journey. Humans are born with a capacity to make judgments and to reason about length, area, volume, etc. as well as a capacity to compare sizes of collections. Each capacity leads directly to a number concept, but to different ones: real numbers and counting numbers, respectively.

Which is better

If learning is based on the acquisition of spontaneous concepts, starting with counting, the familiar sequence from natural numbers up to the rational numbers emerges automatically. But the step to real numbers is a difficult one, both mathematically (it was not until the late nineteenth century that mathematicians really figured out that step) and cognitively (“filling in the holes in the rational line” is hard to swallow when the rational line appears not to have any holes—being what mathematicians refer to as “dense”.) With geometry (and trigonometry) no longer in vogue, the US curriculum neatly avoids the issue of what real numbers are (wisely in my view) by shifting gear at that point and sneaking in the real number system under the heading “algebra”, where the focus is on procedural matters rather than conceptual ones. (Complex numbers still remain problematical, and in fact are generally introduced, usually at college level, as a scientific concept (which is surely what it is), motivated by procedural demands.)

Clearly, the Davydov approach has no such difficulties. With the real number system as basic, integers and rational numbers are just particular points on the real number line.

Another possible advantage of the Davydov approach is that the more troublesome problems about how to successfully introduce multiplication and division that plague the start-with-counting approach to learning math—the focus of three of my columns last year—simply do not arise, since multiplication and division are natural concepts in the world of lengths, volumes, masses, etc. and part-whole relationships between them.

One feature of the Davydov approach that I personally (as a mathematician, remember, not a teacher or an expert in mathematics education, which I am not) find worrying is the absence of exercise sets focused on specific skills. Chunking and the acquisition of procedural fluency are crucial requirements for making progress in mathematics, and I don’t know of any way to achieve that than through repetitive practice. While a math curriculum that consists of little else than repetitive exercises would surely turn many more students off math than it would produce skilled numbers people, there absence seems to me just as problematic. A colleague in mathematics education tells me that Russian teachers sometimes (often?) do get their pupils to work through focused, repetitive exercise sets, and I wonder if success with a more strict Davydov curriculum might depend at least in part on parents working on repetitive exercises with their children at home.

Whether one approach is, overall, inherently better than the other, however, I simply do not know. Absent lots of evidence, no one knows. Unfortunately—and that’s a mild word to use given the high stakes of the math ed business in today’s world—there haven’t been anything like enough comparative studies to settle the matter.

One of the few US-based studies I am aware of involved an implementation of the entire three years of Davydov’s elementary mathematics curriculum in a New York school. The study was led by Jean Schmittau of the State University of New York at Binghamton. Schmittau (2004, p.20) reports that “the children in the study found the continual necessity to problem solve a considerable—even daunting—challenge, which required virtually a year to meet, as they gradually developed the ability to sustain the concentration and intense focus necessary for success. However, upon completion of the curriculum, they were able to solve problems normally given only to US high school students.”

Countering commonly made claims that in the era of cheap electronic calculators, there is no need for children to learn how to compute, and that time spent on computation actually hinders conceptual mathematical learning (for instance, you’ll find these claims made repeatedly in the 1998 NCTM Yearbook), Schmittau writes (2004, p.40), “In light of the results presented [in her paper], it is impossible to subscribe to the contention that conceptualization and the ability to solve difficult problems, are compromised by learning to compute. Not only did the children using Davydov’s curriculum attain high levels of both procedural competence and mathematical understanding, they were able to analyze and solve problems that are typically difficult for US high school students. They did not use calculators, and they resolved every computational error conceptually, without ever appealing to a “rule”. In addition, developing computational proficiency required of them both mathematical thinking and the establishing of new connections – the sine qua non of meaningful learning.”

Here again, I find myself worrying about the balance between, on the one hand, deep conceptual understanding and the ability to reason from first principles—highly important features of doing math – and, on the other hand, the need for rule-based, algorithmic methods that are practiced to the point of automatic fluency in order to progress further in the subject. The continued popularity—with parents if not their children—of commercially-offered, Saturday morning, math-skills classes suggests that I am not alone in valuing basic skills acquisition (procedural fluency), and as I mentioned once already, I often wonder if the success of some curricular experiments does not depend in part on unreported activities outside the classroom.

Another US atudy was carried out at the same time at two schools in Hawai’i by Barbara J. Dougherty and Hannah Slovin of the University of Hawai’i, and there too the researchers reported a successful outcome. They write (2004, p.301),

“Student solution methods strongly suggest that young children are capable of using algebraic symbols and generalized diagrams to solve problems. The diagrams and associated symbols can represent the structure of a mathematical situation and may be applied across a variety of settings.”

(The students used algebraic symbols coupled with diagrammatic representations like the inverted-V diagram shown above. The children in the study referred to in this quote were in the third grade.)

The secret sauce?

These two studies are encouraging. But as with all educational studies, I think we need to be cautious in interpreting them, especially if the goal is to establish educational policy and curricula. (That was not the goal of the two studies I just cited.) One issue is that studies of trial curricula—or “nonstandard” curricula that are being tested—often produce good results, for the simple reason that they are being developed and taught by enthusiastic, knowledgeable experts, with a deep understanding of the material and of educational practice. As a result, what is being measured is arguably the quality of the teaching, not the curriculum.

On the other hand, comparisons of the national performance levels achieved by nationwide curricula are also not conclusive. For instance, pupils in Singapore scored higher than the Russian students on the TIMSS, and Singapore mathematics instruction is based on counting, but not all Russian students are taught by the Davydov approach, so exactly what is being compared with what? Even if the Davydov approach is in some sense inherently superior—and when taken as a whole I think it may well be (in significant part because of the structured, integrated, exploratory way the material is introduced), the consistent high achievement of students in Singapore and Japan suggests that a counting-based approach can work just fine if taught well. (Note that the Singapore and Japanese curricula are also built on a highly structured approach that emphasizes the relationship between concepts. Both countries also place major emphasis on understanding proportionality, which is something the Davydov approach also develops, albeit in a different way.)

In fact, if we pursue that last observation a bit, we get to what I suspect is the really important factor here: teachers who have a deep understanding of basic mathematics. Hmmm, now where have I heard (and read) that before? Liping Ma, anyone?

In fact, in the context of this country, bedeviled by the incessant math wars and the intense politicization of mathematics education that drives them, my view is that debate about the curriculum and the educational theory that drives it is a distraction best avoided (at least for now). To me the real issue facing us is a starkly simple one: Teacher education. No matter what the curriculum, and regardless of the psychological and educational theory it is built upon, teaching comes down to one human being interacting with a number of (usually) younger, other human beings. If that teacher does not love what he or she is teaching, and does not understand it, deeply and profoundly, then the results are simply not going to come. The solution? Attract the best and the brightest to become mathematics teachers, teach them well, pay them at a level commensurate with their training, skills, and responsibilities, and provide them with opportunities for continuous professional development. Just what we do in (for example) the medical or engineering professions. It’s that simple.

Sources

The main source for primary materials on the Davydov curriculum is:

L. P. Steffe, (Ed.), Children’s capacity for learning mathematics. Soviet Studies in the Psychology of Learning and Teaching Mathematics, Vol. VII, Chicago: University of Chicago. Specific articles in that volume are listed below.

My brief summary of the Davydov approach is based primarily on Dougherty & Slovin 2004 and on Schmittau 2004.

The Dougherty & Slovin article describes a US-based (Hawaii) research and development project called Measure Up that uses the Davydov approach to introduce mathematics through measurement and algebra in grades 1-3.

References

Butterworth, B. (1999). What Counts: How Every Brain is Hardwired for Math, Free Press

Davydov, V.V. (1966). Logical and psychological problems of elementary mathematics as an academic subject. From D. B. Elkonin & V. V. Davydov (eds.), Learning Capacity and Age Level: Primary Grades, (pp. 54-103). Moscow: Prosveshchenie.

Davydov, V.V. (1975a). Logical and psychological problems of elementary mathematics as an academic subject. In L. P. Steffe, (Ed.), Children’s capacity for learning mathematics. Soviet Studies in the Psychology of Learning and Teaching Mathematics, Vol. VII (pp.55-107). University of Chicago.

Davydov, V.V. (1975b). The psychological characteristics of the “prenumerical” period of mathematics instruction. In L. P. Steffe, (Ed.), Children’s capacity for learning mathematics. Soviet Studies in the Psychology of Learning and Teaching Mathematics, Vol. VII (pp.109-205). University of Chicago.

Davydov, V. V., Gorbov, S., Mukulina, T., Savelyeva, M., & Tabachnikova, N. (1999). Mathematics. Moscow Press.

Dehaene, S. (1997). The Number Sense: How the Mind Creates Mathematics, Oxford University Press.

Devlin, K. (2000). The Math Gene: How Mathematical Thinking Evolved And Why Numbers Are Like Gossip, Basic Books.

Dougherty, B. & Slovin, H. Generalized diagrams as a tool for young children’s problem solving. Proceedings of the 28th Conference of the International Group for the Psychology of Mathematics Education, 2004, Vol 2 (pp.295-302). PME: Capetown, South Africa.

Ma, Liping, (1999). Knowing and Teaching Elementary Mathematics: Teachers’ Understanding of Fundamental Mathematics in China and the United States, Lawrence Erlbaum: Studies in Mathematical Thinking and Learning.

Morrow, L.J. & M.J. Kenney, M.J. (Eds,) (1998), NCTM Yearbook: The teaching and learning of algorithms in school mathematics. Reston, VA: National Council of Teachers of Mathematics.

Schmittau, J. Vygotskian theory and mathematics education: Resolving the conceptual-procedural dichotomy. European Journal of Psychology of Education, 2004, Vol.XIX, No 1(pp.19-43). Instituto Superior de Psicologia Aplicada : Lisbon, Spain.

Vygotsky, L. (1978). Mind in society: The development of higher psychological processes. Harvard Press.

Devlin’s Angle is updated at the beginning of each month.

Mathematician Keith Devlin (email: devlin@stanford.edu) is the Executive Director of the Human-Sciences and Technologies Advanced Research Institute (H-STAR) at Stanford University and The Math Guy on NPR’s Weekend Edition. His most recent book is The Unfinished Game: Pascal, Fermat, and the Seventeenth-Century Letter that Made the World Modern, published by Basic Books.

FEBRUARY 2009

When the evidence deceives us

A few minutes calculation shows that the quadratic polynomial

generates prime numbers as values for n = 0, 1, 2, … , 39, an unbroken sequence of the first forty natural number arguments. This seems to have been noticed first by Leonard Euler in 1772. Knowing that mathematics is the science of patterns, it is tempting to conclude that the formula generates primes for all natural number arguments, but this is not the case: f(40) is composite, as are many other values.

A mathematician with some experience with prime numbers is unlikely to be “fooled” by the numerical evidence in this example, but even world-class mathematicians have on occasion been misled by far fewer cases; Pierre de Fermat among them. The nth Fermat number F(n) is obtained by raising 2 to the power n, then raising 2 to that number and adding 1 to the result, i.e.

Thus F(0) = 3, F(1) = 5, F(2) = 17, F(3) = 257, F(4) = 65,537.

These numbers are called Fermat numbers because of a claim made by Fermat in a letter written to Mersenne in 1640. Having noted that each of the numbers F(0) to F(4) is prime, Fermat wrote:

“I have found that numbers of the form F(n) are always prime numbers and have long since signified to analysts the truth of this theorem.”

For all his great abilities with numbers, however, Fermat was wrong. This was first shown conclusively by the great Swiss mathematician Leonhard Euler in 1732: F(5) = 4,294,967,297 is not prime. In fact, no prime Fermat number has been found beyond F(4).

There are many other examples where the numerical evidence can mislead us. If you have access to a computer algebra system or a multi-precision scientific calculator program (several of which you can download for free from the Web), try computing

to 30 places of accuracy. You will obtain the result 262 537 412 640 768 744 . 000 000 000 000

An integer! Amazing. Assuming you are aware of Euler’s famous identity

where exponentiation of a transcendental real number by a transcendental imaginary number yields an integer result, you might be surprised that you never came across this other one before. How come you missed it?

The answer is, the result is not an integer. Twelve decimal places all equal to zero is highly suggestive, but if you increase the precision of the calculation to 33 places, you find that

This is still an interesting answer, and you would be right to suspect that there is something special about that number 163 that makes this particular power of e so close to an integer, but I won’t go into that here. My point is simply to illustrate that computation can sometimes lead to conclusions that turn out to be incorrect. In this case the error lies in mistaking for an integer a number that is in fact transcendental.

Another coincidence, in this case most likely having no mathematical explanation, is that to ten significant figures

Here is another example where the numbers can be misleading. If you use a computer algebra system to evaluate the infinite sum

you will get the answer 1. (The half-brackets denote the “largest integer less than or equal to” function.)

But this answer is only approximate. The series actually converges to a transcendental number, which to 268 decimal places is equal to 1. In other words, you would need to calculate the numerical value to at least 269 places to determine that it is not 1, although to ensure there were no rounding errors, you would have to carry out the calculation to an even greater accuracy.

Or try this one on for size (and what a size it is in terms of accuracy). The following “equality” is correct to over half a billion digits:

But this sum, far from being an integer (conceptually far, that is!), is provably irrational, indeed transcendental. As you have probably guessed, this is a “cooked” example, related to my second example. But what an example it is!

The Mertens conjecture

A famous, and mathematically important example where the numerical evidence was misleading is the Mertens conjecture.

If you take any natural number n, then, by the fundamental theorem of arithmetic, either n is prime or else it can be expressed as a product of a unique collection of primes. For instance, for the first five non-primes,

4 = 2 x 2, 6 = 2 x 3, 8 = 2 x 2 x 2, 9 = 3 x 3, 10 = 2 x 5.

Of these, 4, 8, and 9 have prime decompositions in which at least one prime occurs more than once, while in the decompositions of 6 and 10 each prime occurs once only. Numbers divisible by the square of a prime (such as 4, 8, 9) are called square-divisible. Numbers not so divisible are called square-free. (Thus, in the prime decomposition of a square-free number, no prime will occur more than once.)

If n is a square-free natural number that is not prime, then it is a product of either an even number of primes or an odd number of primes. For example, 6 = 2 x 3 is a product of an even number of primes, while 42 = 2 x 3 x 7 is a product of an odd number of primes.

In 1832, A.F. Moebius introduced the following simple function (nowadays called the Moebius function) to indicate what type of prime factorization a number n has.

Let m(1) = 1, a special case. For all other n, m(n) is defined as follows:

If n is square-divisible, then m(n) = 0;

If n is square-free and the product of an even number of primes, then m(n) = 1;

If n is either prime, or square-free and the product of an odd number of primes, then m(n) = –1.

For example, m(4) = 0, m(5) = -1, m(6) = 1, m(42) = -1.

For any number n, let M(n) denote the result of adding together all values of m(k) for k less than or equal to n.

For example, M(1) = 1, M(2) = 0, M(3) = –1, M(4) = –1, M(5) = –2.

At tbis stage, you may like to investigate this question: What is the first value of n beyond 2 for which M(n) is zero again? Or positive again?

So far, everything looks like a nice example of elementary recreational mathematics. Matters take a decidedly more serious turn when you learn that the behavior of the function M(n) is closely related to the location of the zeros of the Riemann zeta function.

The connection was known to T.J. Stieltjes. In 1885, in a letter to his colleague C. Hermite, he claimed to have proved that no matter how large n may be, |M(n)|, the absolute value of M(n), is always less than SQRT(n).

If what Stieltjes claimed had been true, the truth of the Riemann hypothesis would have followed at once. Needless to say, then, Stieltjes was wrong in his claim, though at the time this was not at all clear. (For instance, when Hadamard wrote his now-classic and greatly acclaimed paper proving the Prime Number Theorem in 1896, he mentioned that he understood Stieltjes had already obtained the same result using his claimed inequality, and excused his own publication on the grounds that Stieltjes’ proof had not yet appeared!)

The fact that Stieltjes never did publish a proof might well suggest that he eventually found an error in his argument. At any rate, in 1897, F. Mertens produced a 50-page table of values of m(n) and M(n) for n up to 10,000, on the basis of which he was led to conclude that Stieltjes’ inequality was “very probable.” As a result Stieltjes’ inequality became known as the Mertens Conjecture. By rights, it should have been called the Stieltjes conjecture, of course, but Mertens certainly earned his association with the problem by hand-computing 10,000 values of the function.

When mathematicians brought computers into the picture, they took Mertens’ computation considerably further, eventually calculating 7.8 billion values, all of which satisfied Stieltjes’ inequality. Given such seemingly overwhelming numerical evidence, one might be forgiven for assuming the Mertens conjecture were true, but in October 1983, Hermann te Riele and Andrew Odlyzko brought eight years of collaborative work to a successful conclusion by proving otherwise.

Their result was obtained by a combination of classical mathematical techniques and high-powered computing. The computer was not used to find a number n for which |M(n)| equals or exceeds SQRT(n). Even to date, no such number has been found, and the available evidence suggests that there is no such n below 10³⁰. Rather, they took a more circuitous route. Far too circuitous to present here, in fact. If you want to see exactly what they did, read the account in my book Mathematics: The New Golden Age, Columbia University Press 1999, pp.208-213.

Humbled but not undaunted, however, …

Examples such as the above serve as salutary reminders that when our goal is mathematical truth (certainty), numerical evidence is often at best suggestive. How much higher we set the bar in mathematics than in, say, physics, where ten decimal places of agreement between theory and experiment is generally regarded as conclusive, indeed far more than physicists usually have to settle for.

On the other hand, mathematics is for the most part far less mischievous (and hence potentially far closer to physics) than my above examples might suggest. In general, provided we exercise some reasonable caution, we can, in the words of Yogi Berra, learn a lot by just looking. Looking for, and at, computational (often numerical) evidence, that is.

In today’s era of fast, interactive computers, with computational tools such as Mathematica and Maple—not to forget search engines such as Google—we can approach some areas of mathematics in a way reminiscent of our colleagues in the natural sciences. We can make observations, collect data, and perform (computational) experiments. And we can draw conclusions based on the evidence we have obtained.

The result is a relatively new area (or form) of mathematics called Experimental Mathematics. Proof has a place in experimental mathematics, since computation can sometimes generate insights that lead to proofs. But the experimental mathematician is also willing to reach a conclusion based on the weight of evidence available. I shall say more about this new way of doing mathematics next month—when I will also note that it is actually not quite as new as might first appear.

Devlin’s Angle is updated at the beginning of each month.

MARCH 2009

What is Experimental Mathematics?

In my last column, I gave some examples of mathematical hypotheses that, while supported by a mass of numerical evidence, nevertheless turn out to be false. Mathematicians know full well that numerical evidence, even billions of cases, does not amount to conclusive proof. No matter how many zeros of the Riemann Zeta function are computed and observed to have real-part equal to 1/2, the Riemann Hypothesis will not be regarded as established until an analytic proof has been produced.

But there is more to mathematics than proof. Indeed, the vast majority of people who earn their living “doing math” are not engaged in finding proofs as all; their goal is to solve problems to whatever degree of accuracy or certainty is required. While proof remains the ultimate, “gold standard” for mathematical truth, conclusions reached on the basis of assessing the available evidence have always been a valid part of the mathematical enterprise. For most of the history of the subject, there were significant limitations to the amount of evidence that could be gathered, but that changed with the advent of the computer age.

For instance, the first published calculation of zeros of the Riemann Zeta function dates back to 1903, when J.P. Gram computed the first 15 zeros (with imaginary part less than 50). Today, we know that the Riemann Hypothesis is true for the first ten trillion zeros. While these computations do not prove the hypothesis, they constitute information about it. In particular, they give us a measure of confidence in results proved under the assumption of RH.

Experimental mathematics is the name generally given to the use of a computer to run computations—sometimes no more than trial-and-error tests—to look for patterns, to identify particular numbers and sequences, to gather evidence in support of specific mathematical assertions, that may themselves arise by computational means, including search.

Had the ancient Greeks (and the other early civilizations who started the mathematics bandwagon) had access to computers, it is likely that the word “experimental” in the phrase “experimental mathematics” would be superfluous; the kinds of activities or processes that make a particular mathematical activity “experimental” would be viewed simply as mathematics. On what basis do I make this assertion? Just this: if you remove from my above description the requirement that a computer be used, what would be left accurately describes what most, if not all, professional mathematicians have always spent much of their time doing!

Many readers, who studied mathematics at high school or university but did not go on to be professional mathematicians, will find that last remark surprising. For that is not the (carefully crafted) image of mathematics they were presented with. But take a look at the private notebooks of practically any of the mathematical greats and you will find page after page of trial-and-error experimentation (symbolic or numeric), exploratory calculations, guesses formulated, hypotheses examined, etc.

The reason this view of mathematics is not common is that you have to look at the private, unpublished (during their career) work of the greats in order to find this stuff (by the bucketful). What you will discover in their published work are precise statements of true facts, established by logical proofs, based upon axioms (which may be, but more often are not, stated in the work).

Because mathematics is almost universally regarded, and commonly portrayed, as the search for pure, eternal (mathematical) truth, it is easy to understand how the published work of the greats could come to be regarded as constitutive of what mathematics actually is. But to make such an identification is to overlook that key phrase “the search for”. Mathematics is not, and never has been, merely the end product of the search; the process of discovery is, and always has been, an integral part of the subject. As the great German mathematician Carl Friedrich Gauss wrote to his colleague Janos Bolyai in 1808, “It is not knowledge, but the act of learning, not possession but the act of getting there, which grants the greatest enjoyment.”

In fact, Gauss was very clearly an “experimental mathematician” of the first order. For example, his analysis—while still a child—of the density of prime numbers, led him to formulate what is now known as the Prime Number Theorem, a result not proved conclusively until 1896, more than 100 years after the young genius made his experimental discovery.

For most of the history of mathematics, the confusion of the activity of mathematics with its final product was understandable: after all, both activities were done by the same individual, using what to an outside observer were essentially the same activities—staring at a sheet of paper, thinking hard, and scribbling on that paper. But as soon as mathematicians started using computers to carry out the exploratory work, the distinction became obvious, especially when the mathematician simply hit the ENTER key to initiate the experimental work, and then went out to eat while the computer did its thing. In some cases, the output that awaited the mathematician on his or her return was a new “result” that no one had hitherto suspected and might have no inkling how to prove.

What makes modern experimental mathematics different (as an enterprise) from the classical conception and practice of mathematics is that the experimental process is regarded not as a precursor to a proof, to be relegated to private notebooks and perhaps studied for historical purposes only after a proof has been obtained. Rather, experimentation is viewed as a significant part of mathematics in its own right, to be published, considered by others, and (of particular importance) contributing to our overall mathematical knowledge. In particular, this gives an epistemological status to assertions that, while supported by a considerable body of experimental results, have not yet been formally proved, and in some cases may never be proved. (It may also happen that an experimental process itself yields a formal proof. For example, if a computation determines that a certain parameter p, known to be an integer, lies between 2.5 and 3.784, that amounts to a rigorous proof that p = 3.)

When experimental methods (using computers) began to creep into mathematical practice in the 1970s, some mathematicians cried foul, saying that such processes should not be viewed as genuine mathematics—that the one true goal should be formal proof. Oddly enough, such a reaction would not have occurred a century or more earlier, when the likes of Fermat, Gauss, Euler, and Riemann spent many hours of their lives carrying out (mental) calculations in order to ascertain “possible truths” (many but not all of which they subsequently went on to prove). The ascendancy of the notion of proof as the sole goal of mathematics came about in the late nineteenth and early twentieth centuries, when attempts to understand the infinitesimal calculus led to a realization that the intuitive concepts of such basic concepts as function, continuity, and differentiability were highly problematic, in some cases leading to seeming contradictions. Faced with the uncomfortable reality that their intuitions could be inadequate or just plain misleading, mathematicians began to insist that value judgments were hitherto to be banished to off-duty chat in the university mathematics common room and nothing would be accepted as legitimate until it had been formally proved.

What swung the pendulum back toward (openly) including experimental methods, was in part pragmatic and part philosophical. (Note that word “including”. The inclusion of experimental processes in no way eliminates proofs.)

The pragmatic factor behind the acknowledgment of experimental techniques was the growth in the sheer power of computers, to search for patterns and to amass vast amounts of information in support of a hypothesis.

At the same time that the increasing availability of ever cheaper, faster, and more powerful computers proved irresistible for some mathematicians, there was a significant, though gradual, shift in the way mathematicians viewed their discipline. The Platonistic philosophy that abstract mathematical objects have a definite existence in some realm outside of Mankind, with the task of the mathematician being to uncover or discover eternal, immutable truths about those objects, gave way to an acceptance that the subject is the product of Mankind, the result of a particular kind of human thinking.

The shift from Platonism to viewing mathematics as just another kind of human thinking brought the discipline much closer to the natural sciences, where the object is not to establish “truth” in some absolute sense, but to analyze, to formulate hypotheses, and to obtain evidence that either supports or negates a particular hypothesis.

In fact, as the Hungarian philosopher Imre Lakatos made clear in his 1976 book Proofs and Refutations, published two years after his death, the distinction between mathematics and natural science—as practiced—was always more apparent than real, resulting from the fashion among mathematicians to suppress the exploratory work that generally precedes formal proof. By the mid 1990s, it was becoming common to “define” mathematics as a science—”the science of patterns”.

The final nail in the coffin of what we might call “hard-core Platonism” was driven in by the emergence of computer proofs, the first really major example being the 1974 proof of the famous Four Color Theorem, a statement that to this day is accepted as a theorem solely on the basis of an argument (actually, today at least two different such arguments) of which a significant portion is of necessity carried out by a computer.

The degree to which mathematics has come to resemble the natural sciences can be illustrated using the example I have already cited: the Riemann Hypothesis. As I mentioned, the hypothesis has been verified compuationally for the ten trillion zeros closest to the origin. But every mathematician will agree that this does not amount to a conclusive proof. Now suppose that, next week, a mathematician posts on the Internet a five-hundred page argument that she or he claims is a proof of the hypothesis. The argument is very dense and contains several new and very deep ideas. Several years go by, during which many mathematicians around the world pore over the proof in every detail, and although they discover (and continue to discover) errors, in each case they or someone else (including the original author) is able to find a correction. At what point does the mathematical community as a whole declare that the hypothesis has indeed been proved? And even then, which do you find more convincing, the fact that there is an argument—which you have never read, and have no intention of reading—for which none of the hundred or so errors found so far have proved to be fatal, or the fact that the hypothesis has been verified computationally (and, we shall assume, with total certainty) for 10 trillion cases? Different mathematicians will give differing answers to this question, but their responses are mere opinions.

With a substantial number of mathematicians these days accepting the use of computational and experimental methods, mathematics has indeed grown to resemble much more the natural sciences. Some would argue that it simply is a natural science. If so, it does however remain, and I believe ardently will always remain, the most secure and precise of the sciences. The physicist or the chemist must rely ultimately on observation, measurement, and experiment to determine what is to be accepted as “true,” and there is always the possibility of a more accurate (or different) observation, a more precise (or different) measurement, or a new experiment (that modifies or overturns the previously accepted “truths”). The mathematician, however, has that bedrock notion of proof as the final arbitrator. Yes, that method is not (in practice) perfect, particularly when long and complicated proofs are involved, but it provides a degree of certainty that the natural sciences rarely come close to.

So what kinds of things does an experimental mathematician do? (More precisely, what kinds of activity does a mathematician do that classify, or can be classified, as “experimental mathematics”?) Here are a few:

Symbolic computation using a computer algebra system such as Mathematica or Maple
Data visualization methods
Integer-relation methods, such as the PSLQ algorithm
High-precision integer and floating-point arithmetic
High-precision numerical evaluation of integrals and summation of infinite series
Iterative approximations to continuous functions
Identification of functions based on graph characteristics.

Want to know more? As a mathematician who has not actively worked in an experimental fashion (apart from the familiar trial-and-error playing with ideas that are part and parcel of any mathematical investigation), I did, and I recently had an opportunity to learn more by collaborating with one of the leading figures in the area, the Canadian mathematician Jonathan Borwein, on an introductory-level book about the subject. The result was published recently by A.K. Peters: The Computer as Crucible: An Introduction to Experimental Mathematics. This month’s column is abridged from that book.

We both hope you enjoy it.

Devlin’s Angle is updated at the beginning of each month.

Mathematician Keith Devlin (email: devlin@stanford.edu) is the Executive Director of the Human-Sciences and Technologies Advanced Research Institute (H-STAR) at Stanford University and The Math Guy on NPR’s Weekend Edition. His most recent book for a general reader is The Unfinished Game: Pascal, Fermat, and the Seventeenth-Century Letter that Made the World Modern, published by Basic Books.

APRIL 2009

Stanislaw Ulam—a Great American

This month (April 3, to be precise) marks the 100th anniversary of the birth of one of the most remarkable and influential men of the twentieth century: Stanislaw Ulam.

Ulam was a brilliant Polish mathematician who came to this country at the start of the Second World War, became a leading figure in the Manhattan Project at Los Alamos, New Mexico, the top secret project to develop the nuclear weapon that ended that war, and, together with Edward Teller, worked out the design of the thermonuclear weapons that were at the heart of the Cold War. But inventing the H-bomb was just one of many remarkable things he did.

He was one of those amazing people who did important work in many areas of mathematics—number theory, set theory, ergodic theory, and algebraic topology.

But his real strength was in his incredible ability to see things in a novel way. For example, during the war, when he was at the University of Wisconsin, his friend John von Neumann invited him to join him on a secret project in New Mexico. But he wouldn’t say what it was. So Ulam went to the university library and checked out a book on New Mexico, and looked at the book’s check-out card. It listed the names of all the scientists who had mysteriously disappeared from the university, and by looking at what they were experts in, Ulam was able to figure out what the project was probably about. He himself then joined the Manhattan Project. That was in 1943.

At Los Alamos, Ulam showed Edward Teller’s early model of the hydrogen bomb was inadequate, and suggested a better method. He realized that you could put all the H-bomb’s components inside one casing, stick a fission bomb at one end and thermonuclear material at the other, and use mechanical shock from the fission bomb to compress and detonate the fusion fuel. With a further modification by Teller, who saw that radiation from the fission bomb would compress the thermonuclear fuel much more efficiently than mechanical shock, that became the standard way to build an H-bomb.

It’s a little known fact that Ulam and Teller applied for a patent on their design. I’m not sure if the patent was ever granted, but if it was and you want to build an H-bomb, you’d better make sure you get a license on the patent.

Another Ulam invention at Los Alamos was what we call the Monte Carlo method for solving complicated mathematical problems—originally the integrals that arise in the theory of nuclear chain reactions. The method gets its name from the fact that you use a computer to make lots of random guesses, and then use statistical techniques to deduce the correct answer from all the guesses. It’s a great idea. These days the Monte Carlo method is used all over science and engineering to solve problems that would take too long to solve by other methods.

Perhaps the most amazing of Ulam’s many suggestions was something called nuclear pulse propulsion. This is where you detonate a series of small, directional nuclear explosives against a large steel pusher plate attached to a spacecraft with shock absorbers.

Yes, you heard me right. Don’t be fooled by the fact that this is the April column. This was not only a serious proposal, but it was taken seriously by the US government, who instigated the top-secret Project Orion to build such a spacecraft in the late 1950s and early 1960s.

In theory, such a propulsion system would generate about twelve times the thrust of the Space Shuttle’s main engine. The spacecraft would be a lot bigger than the Shuttle, mind, and could carry over 200 people. It would get to Mars and back in four weeks, compared to 12 months for NASA’s current chemically-powered rocket-craft, and it could visit Saturn’s moons in a seven-month mission, something that would take about nine years using current NASA technologies.

A lot of progress was made during the course of the project, particularly on crew shielding and pusher-plate design, and the system appeared to be entirely workable when the project was shut down in 1965.

Why was it shut down? The main reason given was that the Partial Test Ban Treaty made it illegal.

Some people in the know have since suggested that President Kennedy initiated the Apollo program not only in response to the launch of Sputnik, but also to buy off the people who wanted to continue working on Orion.

Another Ulam idea that attracts a lot of interest these days is one of a number of so-called Singularity Events that have been contemplated. The one that tends to get the most press coverage these days is the supposed date when computers surpass people in intelligence, but Ulam’s singularity is different. In a conversation with von Neumann in 1958, he speculated that, because the progress of technology—and changes in the way we lives our lives—is constantly accelerating, there will come a point when we cannot keep up, and there will be what mathematicians call a singularity. But this time, it won’t be a singularity in a physical system but in human history. So human affairs, as we know them, could not continue. You and I probably won’t experience this. But our children might.

Ulam died in 1984. I never met him, but I did once occupy his office. In 1965, Ulam became a professor at the University of Colorado in Boulder, and in 1980 I spent the summer there. Ulam had remained a consultant at Los Alamos ever since the war, and used to spend part of each year there. That’s where he was when I arrived, so his office in the Math Department was available, and they gave it to me.

So what sense of the man did I get from occupying his office? None whatsoever. It was completely empty apart from a single calculus textbook that I assume he had used to teach a course. But on reflection, maybe that does say something about him. When the subject of the invention of nuclear weapons comes up, the names that get bandied about are Oppenheimer and Teller. Ulam is rarely mentioned. Yet his contribution was no less than either of the two others. He was, it seems, a man more interested in the ideas themselves than the public recognition his work could bring him. Certainly, my Boulder colleagues who did know him speak warmly of him. In an era when Britney Spears and Paris Hilton are two of the most famous Americans on the planet, I’ll vote for Stan Ulam as one of the greatest Americans of all time.

Devlin’s Angle is updated at the beginning of each month.

Mathematician Keith Devlin (email: devlin@stanford.edu) is the Executive Director of the Human-Sciences and Technologies Advanced Research Institute (H-STAR) at Stanford University and The Math Guy on NPR’s Weekend Edition. His most recent book for a general reader is The Unfinished Game: Pascal, Fermat, and the Seventeenth-Century Letter that Made the World Modern, published by Basic Books.

MAY 2009

Do you believe in fairies, unicorns, or the BMI?

Keith Devlin on a cycling trip in the UK in 2009

Take a look at the guy in the photo. According to the Centers for Disease Control and Prevention, he is overweight. They base this classification on a number called the body mass index, or BMI. Also overweight, according to this CDC endorsed metric, are athletes and movie stars Kobe Bryant, George Clooney, Matt Damon, Johnny Depp, Brad Pitt, Will Smith, and Denzel Washington. Tom Cruise scored even worse, being classified as downright obese, as was Arnold Shwarzenegger when he was a world champion body-builder. With definitions like that, no wonder Americans think of themselves as having an overweightness epidemic. (Using the CDC’s BMI measure, 66 percent of adults in the United States are considered overweight or obese.)

Yes, it’s that time of year again, when I go for my annual physical. I know the routine. My body mass index regularly comes out at around 25.1, putting me just into the “overweight category,” and the doctor sends me a fact sheet telling me I need to lose weight, exercise more, and watch my diet. Notwithstanding that fact that the person he has just examined has a waist of 32 inches, rides a bicycle in the California mountains between 120 and 160 miles a week, competes regularly in competitive bicycle events up to 120 miles, does regular upper-body work, has a resting pulse of 59 beats per minute, blood pressure generally below 120/80, healthy cholesterol levels, and eats so much broccoli I would not be surprised to wake up one morning to find it sprouting out of my ears.

(Yes, that really is me in the—recent—photo. No, I’m not a “fitness junkie”. And I am certainly not a professional athlete. I’m just a fairly ordinary guy who was lucky to be born with good genes and who likes being outdoors on my bike when the weather is nice, and I have a competitive streak that makes me want to race every now and then. A not atypical Californian academic, in fact.)

Why do we have this annual BMI charade? Why would otherwise well-educated medical professionals ignore the evidence of their own eyes? Because the BMI is one of those all-powerful magic entities: a number. And not just any number, but one that is generated by a mathematical formula. So it has to be taken seriously, right?

Sadly, despite that fact that completion of a calculus course is a necessary prerequisite for entry into medical school, the medical profession often seems no less susceptible than the general population to a misplaced faith in anything that looks mathematical, and at times displays unbelievable naivety when it comes to numbers.

(Actually, my own physician is smarter than that. I chose him because he is every bit as compulsive an outdoorsy, activities person as I am, and he seems to know that the BMI routine we go through is meaningless, though the system apparently requires that he play along and send me the “You need to lose weight and exercise more” letter, despite our having spent a substantial part of the consultation discussing our respective outdoors activities.)

So what is the BMI? A quick web search on “BMI” or “body mass index” will return hundreds of sites, many of which offer calculators to determine your BMI. All you do is feed in your height and your weight, and out comes that magic number. Many of the sites also give you a helpful guide so you can interpret the results. For instance, the CDC website gives these ranges:

below 18.5 = Underweight

18.5 to 24.9 = Ideal

25.0 to 25.9 = Overweight

30.0 and above = Obese

(Tom Cruise, with a height of 5’7″ and weight of 201 lbs, has a body mass index of 31.5, while the younger Schwarzenegger, at just over six feet tall and about 235 pounds, had a BMI over 31. The figures I quote for athletes and movie stars are from data available on the web, and I believe they are accurate, or were when the information was entered.)

Some sites even tell you how this mystical number is calculated:

BMI = weight in pounds/(height in inches x height in inches) x 703

Hmmm. No mention of waist-size here? Or rump? That’s odd. Isn’t the amount of body fat you carry related to the size belt you need to wear or how baggy is the seat of the jeans the belt holds up?

And what about the stuff inside the body? One thing all those “overweight” and “obese” athletes and movie stars have in common is that they have very little fat and a lot of muscle, and possibly also stronger, healthier bones. Now, a quick web-search reveals that mean density figures for these three body component materials are: fat 0.9 gm/ml, muscle 1.06 gm/ml, and bone 1.85. In other words, the less fat you have, and the more your body weight is made up of muscle and bone, the greater the numerator in that formula, and the higher your BMI.

In other words, if you are a fit, healthy individual with little body fat but strong bones and lots of muscle, the CDC (and other medical authorities) will classify you as overweight. Note the absurdity of the whole approach. If I actually did take my physician’s BMI-triggered, form-letter advice and exercise more, I would put on even more muscle and lose even more of what little body fat I have, and my BMI would increase! With a medical profession like that, who needs high cholesterol as an enemy?

Admittedly, those same authorities also say that a male waistline of 40 inches and a female waistline of 35 inches are where “overweight” begins. But this of course is totally inconsistent with their claim that the BMI is a reliable indicator of excess body fat. In contrast, it is consistent with my observation that it is the density of the stuff inside the body that is key, not the body weight. If you ignore that wide variation in densities, then of course you will end up classifying people with 32 inch waists as overweight. Yet this blatant inconsistency does not seem to cause anyone to pause and ask if there is not something just a little odd going on here. Isn’t it time to inject some science into this part of medical practice?

Time to take a look at that BMI formula and ask where it came from. I’ve already noted that it ignores waistline, rump-size, and the different densities of fat, muscle, and bone. Next question: Why does it mysteriously square the height? What possible scientific reason could there be to square someone’s height for heaven’s sake? (Multiplying height by girth at least has some rationale, as it would give an indication of total body volume, but it would put girth into the denominator in the formula, which is not what you want.) But height squared? Beats me.

Then there is that mysterious number 703. Most websites simply state it as if it were some physical constant. A few make the helpful remark that it is a “conversion factor.” But I could not find a single source that explains what exactly it is converting. It did not take long to figure it out, however. The origins of the BMI, of which more later, goes back to a Belgian mathematician. The original formula would thus have been in metric units, say

BMI = weight in kilograms/(height in meters x height in meters)

To give an equivalent formula in lbs and inches, you need to solve the following equation for C

1lb/(1in x 1in) x C = 0.4536kg/(0.0254m x 0.0254m)

which gives C = 703 (to the nearest whole number).

Well that at least explains the 703. Sort of. But given that the formula is self-evidently just a kludge, why not round it to 700. Stating it as 703 gives an air of accuracy the formula cannot possibly merit, and suggests that the folks who promote this piece of numerological nonsense either have no real understanding of numbers or they want to blind us by what they think we will accept as science.

Another question: Why is the original metric formula expressed in terms of kilograms and meters? Why not grams and centimeters? Or some other units? Well, given the scientific absurdity of dividing someone’s weight by the square of their height, it really doesn’t matter what the units are. I suspect the ones chosen were so that the resulting number comes out between 1 and 100, and thus looks reassuringly like a percentage. I’m beginning to suspect my “blind-us-with-science” conspiracy theory may be right after all.

So which clown first dreamt up this formula and why? Well, it was actually no clown at all, but one of the smartest mathematicians in history: the Belgian polymath Lambert Adolphe Jacques Quetelet (1796–1874). Quetelet received a doctorate in mathematics from the University of Ghent in 1819, and went on to do world class work in mathematics, astronomy, statistics, and sociology. Indeed, he was one of the founders of both these last two disciplines, being arguably the first person to use statistical methods to draw conclusions about societies.

It is to Quetelet that we can trace back that important figure in twentieth century society, the “average man.” (You know, the one with 2.4 children.) He (Quetelet, not the average man) realized that the most efficient way to organize society, allocate resources, etc. was to count and measure the population, using statistical methods to determine the (appropriate) “averages”. He looked for mathematical formulas that would correlate, numerically, with those “average citizens.”

(Elementary) statistics being the highly simplistic (but extremely powerful) tool that it is, it is generally not difficult to find simple formulas that correlate pretty well with society’s averages. You just play around with a few variables until you find a formula that fits. If you can provide a scientific rationale for the formula, so much the better, and you are justified in having more confidence in your ability to use the formula predictively. But it is generally enough that your formula is empirically representative. Provided that all you are doing is trying to draw conclusions about society as a whole, that is. Quetelet knew what he was doing. Many since then, including, it appears, the CDC, do not.

The absurdity of using statistical formulas to make any claim about a single individual is made clear by the old joke about the man who had his head in the refrigerator and his feet in the fire: on average he felt fine!

Yet the CDC says, on its website,

“BMI is a reliable indicator of body fatness for people.”

Nonsense. It is off-the-charts unreliable for me and for millions of people like me. True, a few sentences later, the CDC—doubtless at the insistence of their lawyers—says

“However, BMI is not a diagnostic tool.”

You’re telling me! Come on guys, either the BMI is, as you claim, “a reliable indicator of body fatness”, in which case you can so use it, or, as you also admit, it cannot be used to diagnose excess body fat. Which is it to be?

The CDC’s answer becomes clear as we read on. Lest we note the disclaimer that the BMI cannot be used to diagnose excess body fat and demand a more reliable procedure, they immediately go on to mask their legal get-out by claiming,

“Calculating BMI is one of the best methods for population assessment of overweight and obesity. Because calculation requires only height and weight, it is inexpensive and easy to use for clinicians and for the general public. The use of BMI allows people to compare their own weight status to that of the general population.”

I’ll say it again. This statement is completely false; there are several much better methods—some of which the CDC actually lists on its website! The only part of this second statement that I see as having any validity is the very telling admission that the BMI method is inexpensive and easy to use.

There is another problem with the manner in which the CDC and other medical authorities explain the BMI. Notice that the interpretive ranges into the categories underweight, ideal, etc. are given to one decimal place, with equal signs. This suggests a level of precision in the formula that cannot possibly be warranted. (Some sites give two decimal places.) It would at least be more honest to give the ranges like this:

below 19 you are likely to be underweight
between 19 and 25 is the range generally viewed as ideal
between 25 and 30 suggests you may be overweight
if you are above 30 you are likely to be obese

This would not make the formula any less a piece of numerological junk, but at least would indicate that the ranges are just rough guidelines. The only possible reason for giving the ranges in the precise way the CDC does is to try to mislead patients that there is something scientific going on here. It’s a classic example of “lying with numbers.”

So here is the beef (lean, of course). The BMI was formulated, by a mathematician, not a medical physician, to provide a simple, easy-to-apply mathematical formula to give a broad, society-level measure of weight issues. It has absolutely no scientific or medical basis. It is based purely on a crude statistical analysis. It measures a general society trend, it does not predict. Since the majority of people today (and in Quetelet’s time) lead fairly sedentary lives, and are not particularly active, the formula tacitly assumes low muscle mass and high relative fat content. It applies moderately well when applied to such people because it was formulated by focusing on them! Duh!

But this is not science—it’s not even good statistics—and as a result it should not be accepted medical practice, to be regularly flouted as some magical mumbo jumbo and used as a basis for giving advice to patients. (For heavens sake, even seven times Tour de France winner Lance Armstrong’s own Livestrong website provides a BMI calculator, despite the fact that the boss himself, when he first became a world champion cyclist—before chemotherapy for cancer took 20lbs off him—found himself classified as “overweight” by the wretched formula.)

As you might expect, once a piece of numerological nonsense is held up for proper scrutiny, it doesn’t take long before the whole house of cards comes tumbling down. The surprising thing about the BMI is that it has survived for so long (as a diagnostic for individual patients). As I indicated earlier, I suspect that much of the appeal is that it is a single number, easy to calculate, given an air of scientific authority by a mathematical formula, and (just as my earlier quote from the CDC makes clear) it is easier and quicker to base a diagnosis on a number than on properly examining a patient. But at that point you have stopped doing medicine and are just doing kindergarten arithmetic.

The good news is, at last there is hope of some sanity entering the story. The science (the real science) is finally coming. For instance, a study of 33,000 American adults, published recently in the American Journal of Public Health (Vol 96, No.1, January 2006, 173-178), showed that male life expectancy is greatest for BMIs of about 26—overweight under the CDC’s rule, and equivalent to 24 lb extra for the typical man. For women, the study found an optimum BMI of about 23.5, about 7 lbs heavier than the CDC’s standard.

The paper’s author, Dr Jerome Gronniger, a government scientist, concluded that, “I found that the current definitions of obesity and overweight are imprecise predictors of mortality risk.”

“Imprecise predictors”? Gronniger was clearly using “scientific understatement.” It was, after all, a scientific publication. Dr David Haslam, the clinical director of Britain’s National Obesity Forum was more blatant in a statement he made to the Daily Telegraph newspaper: “It’s now widely accepted that the BMI is useless for assessing the healthy weight of individuals.” (My italics.) [In the UK, it’s almost impossible to be sued, and there is no massive lobby of medical insurance companies looking for ways to avoid paying for your medical treatment, so commentators tend to be more forthcoming.]

Of course, any mathematician surely knew what Haslam now confirms the moment he or she took their first look at Quetelet’s formula. It screams “junk math”.

Numbers are one of the most powerful tools we have to understand our world and to improve our lives. But like all powerful tools, when used irresponsibly, they can do more harm than good. Medical professionals have enormous knowledge and experience that we all benefit from. I do regularly go for my annual physical, and for the most part I listen to my physician’s advice. He knows a lot more than I do about the human body and health issues. I trust him—for the most part. But when the BMI comes up, we are definitely into territory where my expertise trumps his, and I can recognize a piece of numerological nonsense when I see it, and as a result I ignore that part of the proceedings. But if trained medical practitioners, backed up by august professional organizations such as a the CDC, are still so over-awed by such rubbish (mathematics does that to people, I see it all the time) that they continue to preach it as if it were gospel, then how can a patient with less mathematical sophistication hope to resist this annual incantation.

Since the entire sorry saga of the BMI was started by a mathematician—one of us—I think the onus is on us, as the world’s experts on the formulation and application of mathematical formulas, to start to eradicate this nonsense and demand the responsible use of our product.

Heavens, next thing we know, some authority will be claiming that the golden ratio is the aspect ratio of the rectangle most pleasing to the human eye. Where will it all end?

After all that, I think I need a good long bike ride over the mountains to bring my blood pressure down.

Devlin’s Angle is updated at the beginning of each month.

Mathematician Keith Devlin (email: devlin@stanford.edu) is the Executive Director of the Human-Sciences and Technologies Advanced Research Institute (H-STAR) at Stanford University and The Math Guy on NPR’s Weekend Edition. His most recent book for a general reader is The Unfinished Game: Pascal, Fermat, and the Seventeenth-Century Letter that Made the World Modern, published by Basic Books.

JUNE 2009

What’s the real story?

STOCKHOLM (AFP) – A 16-year-old Iraqi immigrant living in Sweden has cracked a maths puzzle that has stumped experts for more than 300 years, Swedish media reported on Thursday. In just four months, Mohamed Altoumaimi has found a formula to explain and simplify the so-called Bernoulli numbers, a sequence of calculations named after the 17th century Swiss mathematician Jacob Bernoulli, the Dagens Nyheter daily said.

That was the opening of a news story that landed in my email inbox on 28 May, courtesy of a listserve subscribed to by a (non-mathematical) friend of mine. The story didn’t make a lot of sense, even when I read the entire article. The Bernoulli numbers are not calculations but, as the name indicates, numbers. To be sure, they are important, particularly in number theory, so any discovery involving them is definitely newsworthy, at least in the mathematical world. But, I was not aware of any 300-year-old problem about the Bernoulli numbers that had resisted all attempts at a solution. Nor did I know how exactly a new result might “explain and simplify” them.

So I dug around on the Web for more details. There were a lot of news stories about the topic, but they all said more or less the same as the article I had already seen. Eventually, however, I found a Swedish news Website with an English-language story that was close to the source (Uppsala University).

“Swedish teen tackles centuries-old numbers challenge” was the headline. The story began, “A 16-year-old Iraqi immigrant in central Sweden has single-handedly figured out a formula with Bernoulli numbers that is normally reserved for much more seasoned mathematicians, earning him praise from professors at prestigious Uppsala University.” Ah. Much more believable.

The reporter went on to explain that Altoumaimi, the young high school pupil, had developed some equations involving the Bernoulli numbers. When his school math teachers were unable to tell him whether what he had done was correct, the student contacted a professor at Uppsala University, who, after examining his work, declared that it was indeed correct. Not new, however. As the story continued,

“While it’s not the first time that someone has shown such Bernoulli number relationships, it’s highly unusual for a first year high school student to make his way through the complicated calculations, according to Uppsala University senior maths lecturer Lars-Ake Lindahl.”

Now we have the real story. Not an original result at all. For sure it was an impressive demonstration of mathematical ability from a young high school pupil, whom the mathematical world may well hear a lot more of in future years, and definitely newsworthy. But most of the story that circulated around the press was entirely fabricated. That’s right, literally made up. Sure, it made for a more exciting story, but it wasn’t true! Now, I don’t know about you, but much as though I love to see math in the news, I also like it to be fairly close to the truth.

Notice that I did not say it should be totally accurate. That is simply too much to expect, given the circumstances under which newspapers, in particular, are produced. The journalist is generally not an expert in the domain, has limited time, and has to get the story out regardless of whether she or he has managed to get hold of a helpful expert to check the facts and give a nice quote. Moreover, the research is almost invariably carried out over the phone, which is not the most ideal way to convey mathematics.

With a magazine it’s possible to take a bit more time, but other factors come into play that can lead to errors—even if the writer is a professional mathematician. This has happened to me on a number of occasions. It starts well enough. The editor contacts me asking for a story on a particular topic, say a major new discovery. I have a week or two to produce it and send it off, after which … well, for a long time nothing. During this period, which can stretch over several weeks, the editor is busy soliciting other articles, and looking to produce a balanced magazine.

Then, out of the blue, I get an email or a phone call requesting various changes to my article, perhaps additional material for a sidebar, or a suggestion of illustrations, maybe a caption for a particular illustration. And this time the deadline is short—possibly only one or two days. To make it worse, this task usually lands on my desk when I am already overloaded with other, equally pressing duties. On top of which, I have not given the article a single look since I originally sent it off, and have forgotten the reasons why I wrote the piece the way I did.

Occasionally, my response leads to a rapid flurry of exchanges involving several of the magazine staff. Passages are added, deleted, moved around, lengthened, shortened, and otherwise amended. Sometimes a suggested alteration will come in over the phone, with an on-the-spot response required. Everything moves so fast, the ground is highly fertile for errors to creep in. And they usually do.

On one occasion some years ago, I was writing an article for Discover magazine about a surprising new theorem that marked significant progress toward a possible proof of the Twin Primes Conjecture (that there are infinitely many pairs of prime numbers separated by exactly 2). Somehow, the version that ended up in print, with my name as the author, claimed that the new theorem actually proved the Twin Primes Conjecture. (On that occasion, I finally realized that the error was the result of an entire line of text being dropped when the article was formatted for the actual printed page. I had been sent a PDF file of the final page just prior to publication, so I had probably “seen” the erroneous final version. But I had not spotted the mistake. I read what I thought it said.)

On another occasion, I was writing a piece about the large number of false claims about the Golden Ratio, also for Discover, when a last minute request came in to provide a sidebar deriving the ratio from its definition in terms of subdividing a line segment. With no free time, I hastily did some copying and pasting from a set of old lecture notes from an undergraduate course given many years earlier. “Yes, that’s the one,” I thought, seeing the short algebraic derivation of a number that began 1.61803.

What I had forgotten was that in the course in question, I had provided the students with examples of proofs, some of which were correct, others containing one or more errors. Their task had been to identify the correct arguments and indicate the errors in the false ones. Okay, you can guess the rest. Of course, I was not aware of the error until the day after publication, when my email inbox filled to overflowing with emails that typically began, “Professor Devlin, I am surprised that someone with your experience could make such an elementary mistake.” And of course, it did have to occur in an article devoted to pointing out false claims about the Golden Ratio!

Having written many articles for newspapers and magazines over the years, I’m used to this happening, and the truth is I’m actually surprised I don’t make more such blunders. Faced with a very tight time deadline, it’s all too easy to read what you think the words say, rather than what they actually say.

With those kinds of experiences behind me, I am therefore very forgiving of errors made in mathematics stories by writers who know far less about the subject than I do. On the other hand, there is a big difference between getting something wrong and simply making stuff up, as in the news story about the Swedish high school student. (The real story here was not the solution by a young schoolboy of a problem that had defied the experts for 300 years; it was how a young schoolboy had shown precocious mathematical talent. Altogether very different.)

At the end of the day, however, I don’t think it matters very much if a story does have errors, and even if, within reason (which the Swedish news story is not, in my view), it contains some creative embellishment.

That comment will infuriate many of my colleagues. I know that because I’ve said it before. But I’ll sail on regardless. I learned that lesson from my editor when I first started to write occasional articles for The Guardian newspaper in the UK back in the early 1980s. “A tiny fraction of your readers will understand what the story is about,” he said. “They will spot any errors, and be able to correct them. Some of them will then have the added pleasure of writing to you to point out the mistake.” (He was right on that score!)

“But this is a national newspaper, not a mathematics journal, and people who know some mathematics are not your main audience,” he would say.

“The reader you should focus on is the person who knows nothing about maths. They won’t understand any of the details, but if you write the story in an engaging fashion, they will read to the end and be left with several impressions: (i) that there has been a new development in the subject, (ii) what kind of person or persons made the advance, (iii) what it is about in general terms, (iv) perhaps s sense of why some people chose to do mathematics for a career, and (v) how it may affect their lives.”

(News stories about mathematics almost always include a remark about possible applications precisely to provide this link to the readers’ lives.)

To my mind, taken together, (i) through (v) constitute a home run in terms of reminding people that mathematics is a living, growing subject that is important to society and should continue to be supported. And that’s my main goal in writing for a newspaper.

Oh, and by the way, I made up those quotes. My editor did say something like that, and I took it to heart. But I did not take notes and I forget his actual words. I just thought it would add a human element to my story to format it as a quote. (I even wrote “maths” instead of “math” since, as a New Zealender, he would have used the British form.) So there!

And if you got to this point in my column, I kept your attention right to the end, so it all worked, right? Okay, I realize that, as a reader of MAA Online, you may well have been reading simply to catch me out!

Now, I wonder what error I have made in this article.

Devlin’s Angle is updated at the beginning of each month.

Mathematician Keith Devlin (email: devlin@stanford.edu) is the Executive Director of the Human-Sciences and Technologies Advanced Research Institute (H-STAR) at Stanford University and The Math Guy on NPR’s Weekend Edition. His most recent book for a general reader is The Unfinished Game: Pascal, Fermat, and the Seventeenth-Century Letter that Made the World Modern, published by Basic Books.

JULY 2009

Trisecting Devlin’s Angle

Behind every good writer is a good editor. That point was emphasized time and again by the four instructors (coaches would be a more accurate term) at the MAA PREP workshop on mathematical writing held at the MAA’s Carriage House from June 29 through July 2. Those instructors were Ivars Peterson (who organized the workshop), Paul Zorn, Underwood Dudley, and myself. It was the second year the four of us have given such a workshop, which focused on mathematical writing and editing for a wide variety of audiences and publications, from research journals to national and local newspapers.

Drawing on our many years of experience in mathematical writing, the four of us gave a number of presentations on various aspects of the writing, editing, and publication process, from overall structure of an article or book down to the fine details of copy editing and punctuation. But I think all present would agree that of most value were the intensive group editing sessions, where the participants broke into groups of three or four, each with one of the instructors, to edit drafts of articles they were working on.

My group consisted of three mathematicians interested in writing for general audiences, but each had a different focus. By good fortune, the four of us rapidly developed a wonderful group dynamic, and as we worked through the different drafts articles, I felt that there could be valuable lessons to be learned by people not at the workshop if we could create a public record of our process. The ideal would have been a video of our activities, but that would have required considerable advance planning. So I hit upon the idea of taking the July edition of Devlin’s Angle and letting the group edit it. Since we would all be back at our home locations, joint editing was not really possible, so each group member would have to edit it individually. That would lose much of the dynamic of group editing, but it would, I hoped, illustrate how a piece of writing can benefit by being looked at by another pair of eyes.

The “safe” way would be to go through the whole process and then post the final results online. But being aware of the popular success of TV reality shows such as Survivor, I felt it might be more fun to have the added danger of doing this “live”, without knowing in advance just how it would turn out. One thing this would demonstrate was that a crucial requirement for any editing process to be successful is the willingness of the writer to expose him or herself to the critiques of others—to listen to what they say and be prepared to accept advice. To most of us, this does not come easy, though in my experience, the more times you go through it the easier it gets—primarily because you come to realize just how much better the finished product is as a result. It would be false modesty for me to pretend I do not have a reputation as a “good writer”. But that reputation is built on the largely invisible shoulders of the many excellent editors who have worked with me over the years to turn my initial submitted drafts into the polished pieces everyone gets to see. To be sure, I always go through several iterations of my draft before I let an editor see it. Indeed, what I send in is invariably something that I cannot see how to improve any more. But I know from experience that there is usually a lot more that can be done to improve it.

Devlin’s Angle is a bit different from most other academic writing, in that it is an opinion column. It is meant to have a conversational tone. I deliberately leave it with some rough edges. As I write it, I always imagine myself speaking the words to a friend sitting across from me in a bar. (Ivars told the group he reads all his writing aloud to see how it sounds.) Moreover, it is not edited by anyone else. This month’s issue is different—each Monday for the remainder of July, you will see a freshly edited version.

The Angle trisectors and the rules for trisection

Let me introduce our three Angle trisectors. Katherine Socha is at St. Mary’s College of Maryland. Her main focus at the workshop was writing a book on fractions suitable for students, teachers, and parents. Janet Beery, from the University of Redlands in California, was working on an article about the history of mathematics. And Monica Neagoy is an independent scholar and author from the Washington D.C. area, who is writing an algebra textbook for both students and their parents. (Monica is the person who gets the credit for the great title of this month’s column.) At the workshop, over several intensive meetings, all three proved themselves to be talented writers with well developed styles, as well as natural and creative editors. (If they had not, this month’s experimental column format would not have been possible.) Each contributed in different ways, demonstrating why the mythical lone writer of popular culture—generally locked away and starving in a tiny garret—is really up against it when pitted against the collective talents of a group. We quickly developed the respect and trust required for editing to be successful. We also had a lot of fun working together. I’m looking forward to seeing what they produce.

Here are the rules we agreed to for this exercise. Each week for the remainder of the month, one of them will edit this column, along with a sample draft article by me (see momentarily), with the new versions being published on successive Mondays. They will edit the original version (of both the column and the sample), though of course, as we progress, successive editors can take into account, and incorporate if they wish, changes made by previous editors. Their editing of the main body of the column can range from changes in punctuation to the complete rewriting or even nixing of entire paragraphs. The only constraint is that they tell the same overall story about the workshop and how and why we came to embark on this exercise. (They each get to determine for themselves exactly what this amounts to.) They are all free to take entire passages from the others—it’s not plagiarism in this case, rather collaborative writing over the Internet. (In a for-real case, the final version would have my name at the top, and the editor would get at most a footnote acknowledgement. This is why authors should really value and look forward to the editing process: those editors make you look smart!)

All versions will remain on the website for comparison.

Since most readers who find this month’s topic of interest will likely be motivated by a desire to improve their skills in writing about mathematics (rather than about a workshop), in addition to editing the column, I supplied a short piece I had written about algebra. Here the constraints are a bit different. The intention is to write a short op-ed piece for a local or national newspaper that will explain to parents what algebra is and why their children may be finding it difficult. The title is fixed and the piece has a strict upper limit of 400 words, excluding the title. It has to get past the editor, grab and keep the attention of the readers, and leave them with as good an understanding of algebra and algebra-learning as is possible in just 400 words. In this case, the goal is to improve my article—unlike editing the workshop description, where they can make major changes of they wish. That presents an additional challenge of maintaining the style and voice of the original author. If an editor feels that a passage, or even the entire piece, needs to be re-written, then their response will be to suggest an alternative, which in a for-real case I would then have to recast in my voice. (We won’t do that last step in this exercise. The goal is to demonstrate the process, not the result.) Of course, editors are not obliged to change anything. Part of good editing is knowing when something is fine just as it is. If one of our three editors makes very few changes, that can still indicate good editing. In our group edits, there were plenty of passages in the various drafts the group provided that none of us thought required any changes. Professional editors are generally paid by the overall length of the article, not the number of change they make! Consequently, I always start out assuming an editor is right and I am wrong, and then think about the point. Over the years, I have found that I end up accepting around 90% of an editor’s suggestions, either verbatim or by finding a way of my own to address the issue that elicited the suggested change.

For the record, the sample passage is taken from a slightly longer op-ed piece I wrote a year ago that did not get past the editor (though it did lead to the newspaper writing a substantial article of its own on the topic, in which I was quoted extensively). As a result, I worked on it quite a lot to get it into the best shape I could. It is not a first draft by any means. But it has never been edited by anyone else. Until now.

You will find the first version (mine) of the sample op-ed piece here.

Tune in next week for episode 2.*

* [In re-assembing this post for the archives, I had to restructure it. You’ll see my stuff first (you just did), then in the August post that follows, you’ll see the others.]

Devlin’s Angle is updated at the beginning of each month.

Mathematician Keith Devlin (email: devlin@stanford.edu) is the Executive Director of the Human-Sciences and Technologies Advanced Research Institute (H-STAR) at Stanford University and The Math Guy on NPR’s Weekend Edition. His most recent book for a general reader is The Unfinished Game: Pascal, Fermat, and the Seventeenth-Century Letter that Made the World Modern, published by Basic Books.

AUGUST 2009

In praise of good editors

Blaise Pascal is reported to have once ended a letter with the observation: “I have written you a long letter because I did not have time to write a short one.”

Pascal had it right. Good writing is hard work. Writing that is informative, flows well, is easy to understand (and unlikely to be misunderstood), and is as brief as possible while meeting all those other criteria, takes time and effort. In most cases, it is also the result of at least two minds – the author (who gets the praise, should any be forthcoming) and an editor (who gets at most a single mention in the acknowledgements).

Editing was one of the main discussion points at the PREP workshop on mathematical writing held at the MAA Carriage House in Washington D.C. in June, an event that was the focus of my last column (July).

One of the workshop themes was the importance of editing your own writing—indeed, editing is an integral part of the writing process. Another was the benefit of having your writing edited by someone else. To experience this part of writing, the workshop split into small working groups, each of which took a collective look at samples of writing provided by the members. In my case, the group comprised, in addition to myself, Katherine Socha of St. Mary’s College of Maryland, Janet Beery from the University of Redlands in California, and Monica Neagoy, an independent scholar and author from the Washington D.C. area. My July column—which grew into our column as July progressed and the other three successively edited it—provided a fairly detailed look at our activities as a collaborative group.

All four workshop presenters (Ivars Peterson, Paul Zorn, Underwood Dudley, and myself) had served as editors at one time or another, as had some of the participants. But we were all primarily writers. The focus of the workshop was to improve mathematical writing skills. Our interest in the editing process was motivated by our desires (instructors and participants alike) to become better writers. We were not trying to become professional editors.

Being a professional copy editor requires a very different set of skills than what is required to edit your own work or that of a fellow writer, and few people seem to excel at both.

Over the years, I have worked with a number of first rate professional copy editors. After the first version of my July column appeared, one professional mathematics editor I am acquainted with (we have corresponded a few times, but never met or worked together) could not resist editing the sample newspaper op-ed article our group used as an exercise in editing. I thought it would be of interest to finish off my discussion of editing by showing you (with his kind permission) what he produced.

His name is JD (Joshuah) Fisher, currently living in Cedar Park, Texas. He is the managing editor of a company that provides staff development and middle-school mathematics instruction to school districts throughout the U.S. He has been a mathematics textbook editor and writer for about fourteen years.

The purpose of the exercise was to write a short op-ed piece for a local or national newspaper that will explain to parents what algebra is and why their children may be finding it difficult. The title was fixed and the piece had a strict upper limit of 400 words, excluding the title. It has to get past the editor, grab and keep the attention of the readers, and leave them with as good an understanding of algebra and algebra-learning as is possible in just 400 words. You will find my original sample op-ed piece here.

Fisher’s edited version, complete with mark-ups, is here. (I double-spaced it to make it easier to follow the editor’s comments.)

For comparison, Socha’s edited version is here.

Beery’s edited version is here.

Neagoy’s edited version is here.

As you will see, each of the three “editors” in our PREP group sought some improvements along the lines Fisher did. But none of us came close to his version. Not only did he spot various structural flaws in my composition, he managed to reduce the overall length to just over 350 words. I don’t know about you, but I think Fisher’s version is a lot better than my original. The content is not different, notice. It still says what I set out to say, and it still carries my voice. But it’s just much, much better—cleaner and more to the point. I can’t afford to hire him to edit Devlin’s Angle. But I did once hire him to edit a math book I self-published on Amazon. QED.

Devlin’s Angle is updated at the beginning of each month.

Mathematician Keith Devlin (email: devlin@stanford.edu) is the Executive Director of the Human-Sciences and Technologies Advanced Research Institute (H-STAR) at Stanford University and The Math Guy on NPR’s Weekend Edition. Devlin’s most recent book for a general reader is The Unfinished Game: Pascal, Fermat, and the Seventeenth-Century Letter that Made the World Modern, published by Basic Books.

THREE VERSIONS OF THE JULY POST

Here, in reverse chronological order, are the three versions of my July post produced by the MAA workshop team. KD

NEAGOY’S VERSION

THIS COLUMN HAS BEEN EDITED FIRST BY KATHERINE SOCHA, THEN BY JANET BEERY, AND NOW FINALLY BY MONICA NEAGOY. SCROLL DOWN TO SEE BEERY’S VERSION, SCROLL DOWN FURTHER TO SEE SOCHA’S VERSION, AND SCROLL UP TO THE JULY POST TO SEE DEVLIN’S ORIGINAL.

Trisecting Devlin’s Angle

Know your audience. Find your voice. Have a clear message. Read your prose out loud. Listen to your editor. These were some of the points emphasized at the MAA PREP workshop on expository mathematical writing, held at the MAA Carriage House from June 29 to July 2. Directed by four well-known mathematics writers, Ivars Peterson (workshop organizer), Paul Zorn, Underwood Dudley, and Keith Devlin, fifteen participants explored mathematical writing for a wide range of audiences and publications. Drawing on years of experience, the workshop leaders made presentations on the writing, editing, and publication processes, from the overall structure of an article or book down to the details of copy editing and punctuation.

To you, our diligent readers returning for the final iteration of Devlin’s Angle trisection, writing and editing must be a matter of import. Perhaps because you too wish to expand your reach beyond your students. Or because you are convinced that writing is one of the finest activities known to mankind. Or simply because you are beguiled by this live, online writing/editing process. Whatever the case, here are some gems that our wise and skilled coaches shared with us.Use few adjectives and no adverbs.

Mark Twain would concur. Was it not he who said “substitute ‘damn’ everywhere you’re inclined to write ‘very;’ your editor will delete it and your writing will be just as it should be”? Avoid cliches like the plague. Search and destroy those language fossils!

Here’s one you find everywhere: “Algebra is a gateway course.” Quite apropos. Such metaphors or expressions have become trite through their overuse and are but a testimony of mental sloth or putrefaction.

Write a lot and pare a lot. Write, rewrite, and rewrite again. And only then, after you’ve rewritten to your own liking and approval might you be ready to really write. Don’t say “We shall introduce …” or “I will give an example of …” Just do it! Similarly, don’t say “it is clear that …” or “it is easy to see that…” Just make it so. And don’t ever write “notice that…”! If it’s not noticeable then what are you writing?

Put every word under a microscope. Be discerning. Appreciate the difference between “I hit only him in the eye” and “I hit him only in the eye” or “I hit him in the only eye.” If you put the expression “to write something down” under a microscope, you realize the descent of thought the phrase suggests – from mind to body (hand/fingers). But don’t our ideas come from our consciousness, which resides in every cell of our body? Lakoff and Johnson’s Metaphors We Live By might elucidate.

It’s not about you. Be transparent so the reader can read through you to the material. The mathematics is important. Not yourself. The words that followed this admonition jetted out with the insistence of a stream from a spout: “Mathematics is the most glorious creation of the human intellect so we should treat it with respect and deference.” Agreed. Persevere!

It is said that Richard Bach received 140 rejections of Jonathan Livingston Seagull before it was ultimately published in 1970. By 1972, over a million copies were in print. It soon topped the New York Times Best Seller list where it remained for 38 weeks. If that isn’t perseverance, I don’t know what is.

Behind every good writer is a good editor. If you are hurt by your editor’s remarks, then writing is not for you. If you are obdurate about your work, unwilling to make changes, you may be sacrificing the success of your article or book. Embrace the suggested changes and enjoy the constraints. Remember, your editor sees more clearly; you are too close to your work.

A perfect segue to the most valuable part of the workshop: the intensive group editing sessions. In groups of three or four, coached by one workshop leader, we edited our drafts. The writings ranged from journal articles to children’s books. The Devlin group for example consisted of three mathematicians interested in writing for general audiences. Katherine Socha, of St. Mary’s College of Maryland, focused on a co-authored book on fractions for parents, teachers, and children. Janet Beery, from the University of Redlands in California, worked on an article about the history of mathematics for high school teachers. And I, Monica Neagoy, an independent scholar and author from the Washington DC area, concentrated on an algebra book for all who teach algebra. Keith Devlin both guided and participated in the editing process.

As the four of us edited one another’s work, we quickly developed a wonderful rapport that was both positive and productive. We all had strong opinions yet we were open to the other group members’ suggestions. Probably because we were true to the role of an editor. Good editors make keen suggestions, open your eyes, offer a different perspective, but leave the writing to you. Our experience validated our guest speaker’s words—”The fruit of real collaboration is greater than the sum of its parts”—but contradicted Hemingway’s words—”To talk about your work is … to weaken it, to take away its magic and strength.” Au contraire.

Our experience was so positive that Devlin, the talented multi-tasker, hit upon the idea of using our collaboration as a public exemplar of this important lesson: behind every good writer is a good editor (or team of editors in this case). He suggested that we illustrate the editing process by jointly editing the July edition of Devlin’s Angle. And so, the Angle Trisection process was born. We decided to edit serially and “live.” Each of us agreed to edit both Devlin’s workshop description and mathematical essay, according to specific rules. As all who write for public venues learn, a crucial requirement for success is the willingness of the writer to accept exposure to the criticisms and critiques of others.

The rules for trisection On July 6, Devlin posted his column as well as a draft of an op-ed piece on algebra written for a newspaper. On each subsequent Monday, one of the three trisectors will (1) re-write this column, turning it into a co-authored by Devlin et al., and (2) edit the op-ed piece. Co-authoring the column may range from straightforward editing to wholesale re-writing. The only constraint is that the column must describe the MAA PREP expository writing workshop and the Trisecting Devlin’s Angle project. The Trisectors’ work on the algebra piece however is limited strictly to editing. This part of the exercise aims to illustrate careful editing of an article that is subject to typical newspaper constraints. The title is fixed and the word limit is 400. The goals are to get past the editor, to engage the readers, and to leave editors and readers with a good sense of what algebra and algebraic thinking are. In this exercise, the task is to improve Devlin’s original article. That presents the additional challenge of maintaining the style and voice of the original author while improving on the work itself.

BEERY’S VERSION

Trisecting Devlin’s Angle

Mystery writer Margery Allingham once described a minor character in the novel Dancers in Mourning as a member of the audience who had gotten into the play and who was unabashedly enjoying herself. Fifteen mathematicians “got into the play” at the MAA PREP workshop on expository mathematical writing, held at the MAA Carriage House from June 29 to July 2. Directed by four well-known mathematics writers, Ivars Peterson (workshop organizer), Paul Zorn, Underwood Dudley, and Keith Devlin, participants explored mathematical writing for a wide range of audiences and publications, from MAA journals to local newspapers.

Drawing on their many years of experience in mathematical writing and editing, the four workshop leaders gave a number of presentations on the writing, editing, and publication process, from the overall structure of an article or book down to the fine details of copy editing and punctuation. As useful as these sessions were, everyone agreed that the most valuable part of the workshop was the time allotted to intensive group editing sessions, where the participants broke into groups of three or four, each with one of the leaders, to edit drafts of articles or books they were working on.

Participants’ writing projects ranged from journal articles to children’s books. For instance, the Devlin group consisted of three mathematicians interested in writing for general audiences, but each had a different focus. Katherine Socha, of St. Mary’s College of Maryland, worked on a co-authored book on fractions for parents, teachers, and children. Janet Beery, from the University of Redlands in California, was working on an article about the history of mathematics for high school teachers. Monica Neagoy, an independent scholar and author from the Washington DC area, worked on an algebra book for parents and teachers. Neagoy also gets major ninja props (translation: emphatic kudos) for the great title of this month’s column. Keith Devlin’s job was to both guide and participate in the editing process.

As the four of us edited each other’s work, we quickly developed a wonderful rapport that was both positive and productive. It didn’t take long to convince us of the truth of one of the main messages of the workshop, that any piece of writing, no matter how good, can benefit from being looked at by another pair of eyes or, in this case, three other pairs of eyes. As one of us said at the end of the workshop, “I thought I knew what ‘knowing your audience’ and ‘putting yourself in your readers’ shoes’ meant, but the group editing activity really brought home to me that even the most empathetic writers can benefit from good editing.”

Our experience was so positive that Devlin, always on the lookout for ways to share interesting mathematics and good mathematical practice, hit upon the idea of using our work together as a public example of one of the workshop’s take-home lessons: behind every good writer is a good editor (or team of editors). When he suggested that we illustrate the editing process by jointly editing the July edition of his Devlin’s Angle column, the Angle Trisectors were born. Since the workshop was nearly over and we soon would scatter to our homes around the country, we decided to edit and collaborate serially and “live” online, with one of us submitting edits and rewrites to both the column and a sample piece of mathematical writing, an op-ed piece on school algebra that Devlin had written and never published, each week. With this added challenge, these three workshop participants really have joined in the play!

How can you “get into the play” of expository mathematical writing? Mystery writer Margery Allingham also wrote that “light reading is not light writing,” and expository writing may indeed take more effort and practice than technical writing. So, write early, write often, write widely, write articles, write reviews, write referee’s reports, write doggerel, write as much as you can. Write, write, write. And then … find a good editor.

Read on for the rules the “trisectors” have agreed to follow as they edit and rewrite Devlin’s column and his op-ed piece on school algebra.

The rules for trisection Here are the rules Devlin and his Angle Trisectors will follow for their demonstration of the power of editing and collaboration. On July 6, Devlin posted his column as well as a draft of an op-ed piece written for a local or national newspaper. Each week for the rest of the month, one of the three trisectors will (1) re-write this column, turning it into a co-authored work by her, Devlin, and, if she wishes, any trisectors who have gone before, and (2) edit the associated draft op-ed piece by Devlin.

Co-authoring the column may range from straightforward editing to wholesale re-writing. The only constraint is that the column must describe the MAA PREP expository mathematical writing workshop and the subsequent Trisecting Devlin’s Angle project. The outcomes are unpredictable because we are working serially and onstage (and generally at the last minute) for all the world to see.

Unlike our co-authoring work, the Trisectors’ work on the draft article about algebra is limited strictly to editing. This part of the exercise aims to illustrate careful editing of an article that is subject to typical newspaper constraints. The op-ed piece must explain to parents what algebra is and why children may find it difficult to master. The title is fixed and the body of the work has a strict upper limit of 400 words. The goals are to get past the editor, to grab and keep the attention of the readers, and to leave editors and readers with as good an understanding of algebra and algebraic thinking as is possible in just 400 words. In this exercise, the task is to improve Devlin’s original article. That presents the additional challenge of maintaining the style and voice of the original author while improving on the work itself.

SOCHA’S VERSION

Trisecting Devlin’s Angle

Mystery writer Margery Allingham once described a minor character in the novel Dancers in Mourning as a member of the audience who had gotten into the play and who was unabashedly enjoying herself. Fifteen mathematicians “got into the play” at the Summer 2009 MAA PREP workshop on mathematical writing, led (or, more accurately, coached) by four well-known mathematics writers: Ivars Peterson—director extraordinaire; Paul Zorn—MAA President-elect-elect (sic: his term as President-elect does not begin until January!); Underwood Dudley—veteran editor, writer, and guide; and Keith Devlin—NPR’s Math Guy.

With a range of writing styles from Proustian to Seussian, participants and leaders together spent nearly four days on the writing, editing, and publishing processes, from developing the overall structure of an article or a book to relishing the finer details of copy editing. The workshop included blocks of time dedicated to intensive group editing sessions, organized loosely by type of writing (journal articles, children’s books, writing for general audiences, and textbooks). One workshop leader mentored each group. During these sessions, we all (leaders, too) brought drafts of articles or book chapters for the slightly terrifying prospect of editing our own writing in public.

The Devlin group consisted of three mathematicians interested in writing for general audiences, and each of us had a different focus. Janet Beery, from the University of Redlands in California, was working on an article about the history of mathematics. Monica Neagoy, working on an algebra textbook for both students and parents, is an independent scholar and author from the Washington DC area. (Monica gets major ninja props for the great title of this month’s column.) Katherine Socha, of St. Mary’s College of Maryland, worked on a co-authored book on fractions for parents, teachers, and children. And Keith Devlin’s job was to gauge the state of each project, guide both group and individual progress, and goad the group to finer editing and writing.

As the four of us edited each other’s work, we quickly developed a wonderful rapport that was both positive and productive. Devlin, that talented multi-tasker, hit upon the brilliant idea of using our work together as a public exemplar of the workshop’s take-home lesson: behind every good writer is a good editor (or team of editors). He suggested to the group that we jointly edit the July edition of this column, Devlin’s Angle; but unfortunately, given our limited time, we could not complete the project before scattering to our homes around the country. On the “make lemonade” principle, Devlin convinced us to illustrate the editing and co-writing process serially and online. With the added challenge of editing and co-writing “live” on MAA Online, these three participants really have joined in the play. As all who write for public venues learn over and over, a crucial requirement for success is the willingness of the writer to accept exposure to the criticisms and critiques of others. One deep breath, and here we go!

The rules for trisection Here are the rules Devlin and his Angle Trisectors will follow for this demonstration of the power of co-authoring and the power of editing. Devlin is providing his column as well as a draft of an op-ed article written for a local or national newspaper. Each week for the rest of the month, one of the three will (1) re-write this column, turning it into a co-authored work by Devlin and X, and (2) edit the associated draft op-ed article by Devlin.

Co-authoring the column may range from straightforward editing to wholesale re-writing. In this case, the column – describing the PREP workshop and the subsequent Trisecting Devlin’s Angle project – may evolve to a true co-authorship: the by-line likely will read Beery, Devlin, Neagoy, and Socha. Or three separate columns may be created, with bylines Devlin and Beery, Devlin and Neagoy, and Devlin and Socha. Or two columns may be created, with bylines Devlin and two Trisectors, and Devlin and the third Trisector. The outcomes are unpredictable because we are working serially and onstage for all the world to see.

The revised pieces will be published on successive Mondays. As we progress, successive Trisector editors will edit the original version of both the column and the op-ed article, though each may take into account the work of the previous editors. In this case, it’s not plagiarism, it’s collaborative writing and editing over the Internet.

How can you get into the play? Write early, write often, write widely, write reviews, write articles, write doggerel, write as much as you can. Write, write, write. And then … find a good editor.

AMEN TO THAT LAST OBSERVATION! KD

SEPTEMBER 2009

Reaching out—with style

How can the mathematics community ensure that fewer children are turned off math and more are attracted to it? The people at the NAVET Science Center in the city of Boras, in Sweden, have one answer that I think has the potential to make a huge difference. The city, about an hour’s drive east from the port of Gothenberg, has had for some time a hands-on science museum housed in an old mill. This past year, the museum staff made their way to the second floor, which had hitherto been used only for storage, and turned it into the “Mathematics Palace”. I visited the new palace last month to help celebrate its opening.

I expected to see a mathematically-focused version of the wonderful Exploratorium in my home city of San Francisco. And in a way that is perhaps the best way to think of it. But there is a twist. The organizers had brought in an architectural designer to create the space in which the various hands-on exhibits would be displayed.

The result is that as you enter the Palace, you are immediately overwhelmed by the warm, human elegance of your surrounds. The use of hanging cloth and superb, soft, multicolored lighting adds to the welcome. It would be hard to imagine a space less reminiscent of the popular image of mathematics as being “cold and austere.”

True, that description was coined by a mathematician, Bertrand Russell, but he was talking about an inner beauty of mathematics, seen only by those who put in sufficient effort to penetrate its steely outer walls. To the outsider, “cold and austere” pretty well sums it up in a totally negative, inhuman way. It’s not of course. Mathematics is one of humankind’s greatest creations. But like anything that has depth, you have to see beneath the surface to appreciate what it is really about. And many children (and adults) see no reason why they should bother to look beyond what they see at first glance.

The genius behind the Boras Mathematics Palace (there is an English translation of the homepage text) is that it envelops the mathematical exhibits in a warm and seductively human environment. The exhibits too, while instantly recognizable as “mathematical artifacts” are also constructed with an artistic eye. Take a look for yourself:

Besides the warmth and sheer elegance of the surroundings, the sensations you get as you walk through the space are of history, humanity, and multiculturalness (is there such a word?) In short, it’s what happens when world-famous Scandinavian design meets a hands-on math exhibit.

As a result, not only will the “numbers-averse, arty types” find themselves in comforting, human surroundings, the “who-cares-about-the-design, just-let-me-figure-out-how-this-thing-works” type might just find a growing appreciation of the more artistic side of life. I think the Boras “Palace” serves as a model for how to design such exhibits, that anyone thinking of developing a mathematics museum should experience. Not just read about. Not just look at the photos. Experience. First hand. Because that is what it is all about – a human experience. Check it out for yourself and you’ll see why I am so enthusiastic.

For the record, the organizers did not ask me to write about the Palace, they just wanted me to give a talk at the opening celebration. I’m sharing my experience with you because I think it is such a powerful concept that should be copied all around the world. Admittedly, the result may be that this month’s column reads like bad advertising copy for a vacation. But in this economy, maybe I need to develop a fallback career. Meanwhile, I still think the Boras Mathematics Palace is one of the coolest (and warmest) places I’ve been in for a long time.

Devlin’s Angle is updated at the beginning of each month.

Mathematician Keith Devlin (email: devlin@stanford.edu) is the Executive Director of the Human-Sciences and Technologies Advanced Research Institute (H-STAR) at Stanford University and The Math Guy on NPR’s Weekend Edition. Devlin’s most recent book for a general reader is The Unfinished Game: Pascal, Fermat, and the Seventeenth-Century Letter that Made the World Modern, published by Basic Books.

OCTOBER 2009

Soft mathematics

In my book Goodbye Descartes: The End of Logic and the Search for a New Cosmology of the Mind (John Wiley, 1997), I introduced the term “soft mathematics” to refer to the use of mathematical ideas and ways of thinking in domains that are inherently non mathematical, having observed instances in several disciplines, among them linguistics, psychology, sociology, economics, political science, management science, and intelligence analysis. (You also see instances, generally fictional though sometimes based on fact, in the CBS television crime series Numb3rs.)

I looked at this phenomenon again in my recent article “What will count as mathematics in 2100?” in the MAA Spectrum book Proof and Other Dilemmas: Mathematics and Philosophy, edited by Bonnie Gold and Roger Simons (MAA, 2008, pp.291-311).

So much of my research over the past twenty years has been spent working with experts from other disciplines, in particular in linguistics and in the intelligence analysis community, that I long ago forgot that such uses of some of the notions of mathematics, along with an analytic or design approach based on mathematics, can seem alien to the mathematician. Becoming an expert in a particular discipline (I would like to say “being indoctrinated”, but some might read into that phrase a negative connotation that I do not imply), involves learning to see things in a particular way, and in the process we can “forget” (or never learn) how to see things in other ways.

This tendency to see things in ways we have become familiar with—and to be unable to see distinctions that others take for granted—was brought home to me recently in an email from a group of students in Singapore who were working through Goodbye Descartes and were unable to see why I introduced the term “soft mathematics” for what they saw as plain old “mathematical modeling.”

There is a distinction, and to my eyes it is a big one. But the exchange made it clear that what was clear to me was not necessarily clear to others. (I was reminded of Richard Dawkins, who when asked why so many of his books seemed to be just variations of his original The Selfish Gene, replied that he kept saying the same thing in different ways because people so often failed to understand the points he was trying to make.)

In mathematical modeling, you create a definite model—an equation or system of equations, a set of inequalities, of whatever—that is intended to capture key behavioral features of some worldly domain, and then you do mathematics—of the traditional sort. It looks like mathematics, it smells like mathematics, and by golly it is mathematics. The results may be applied to the world insofar as the model actually does capture the intended features of the world.

Soft mathematics is quite different. There is little or nothing that looks like, or is, traditional mathematics. There may not even be any mathematical symbols tossed around—though in many cases there are. Soft mathematics is not mathematics as that discipline is generally thought of, and it remains an open question whether at some time in the future our conception of what constitutes mathematics will change to incorporate such activities. (I address that question in my MAA Spectrum article referred to above.)

What is clear, however, is that the mathematical way of thinking is such a powerful one that, when applied in a soft manner, it has on occasion led to considerable advances in our understanding of various phenomena in the messy, and decidedly non-mathematical social realm of people. One of the best examples I have come across was in the field of linguistics. I describe this example at some length in Chapter 9 of Goodbye Descartes, from which I have abridged the following shorter account.

Grice’s maxims

In a lecture given at Harvard University in 1967—and subsequently published under the title Logic and Conversation—the logician H. P. (Paul) Grice described a “logic” of everyday conversations, the structure that any conversation must have in order to be successful, regardless of its topic and purpose. He did so by formulating a set of “maxims” (his term) that participants in a conversation implicitly follow. It was a brilliant attempt to apply a mathematical approach to the structure of conversation, very much in the spirit of Euclid’s formulation of axioms for plane geometry.

Grice began his analysis by observing that a conversation is a cooperative act, which the two participants enter into with a purpose. He tried to encapsulate the cooperative nature of conversation by what he called the Cooperative Principle:

Make your conversational contribution such as is required, at the stage at which it occurs, by the accepted purpose or direction of the talk exchange in which you are engaged.

His next step was to derive more specific principles—his maxims—from the Cooperative Principle, by examining consequences under four different headings: quantity, quality, relation, and manner. He illustrated these four categories by means of non-linguistic analogies:

Quantity. If you are assisting a friend to repair his car, your contribution should be neither more nor less than is required; for example, if your friend needs four screws at a particular moment, she expects you to hand her four, not two or six.

Quality. If you and a friend are making a cake, your contributions to this joint activity should be genuine and not spurious. If your friend says he needs the sugar, he does not expect you to hand him the salt.

Relation. Staying with the cake making scenario, your contribution at each stage should be appropriate to the immediate needs of the activity; for example, if your friend is mixing the ingredients, he does not expect to be handed a novel to read, even if it is a novel he would, at some other time, desire to read.

Manner. Whatever joint activity you are engaged in with a friend, your partner will expect you to make it clear what contribution you are making, and to execute your contribution with reasonable dispatch.

In terms of conversation, the category of quantity relates to the amount of information the speaker should provide. In this category, Grice formulated two maxims:

Make your contribution as informative as is required.

Do not make your contribution more informative than is required.

Under the category of quality, Grice listed three maxims, the second two being refinements of the first:Try to make your contribution one that is true.Do not say what you believe to be false.Do not say that for which you lack adequate evidence.

Under the category relation, Grice gave just one maxim:

Be relevant.

Finally, under the category of manner, Grice listed five maxims, a general one followed by four refinements:

Be perspicuous.

Avoid obscurity of expression.

Avoid ambiguity.

Be brief.

Be orderly.

As Grice observed, his maxims are not laws that have to be followed. In that respect they are not like mathematical axioms. If you want to perform an arithmetical calculation in a proper manner, you have to obey the rules of arithmetic (even if you are not consciously aware of so doing). But it is possible to engage in a genuine and meaningful conversation and yet fail to observe one or more of the maxims Grice listed. The maxims seem more a matter of an obligation of some kind. In Grice’s own words:

“I would like to be able to think of the standard type of conversational practice not merely as something which all or most do in fact follow, but as something which it is reasonable for us to follow, which we should not abandon.” [Emphasis as in the original.]

Clearly, Grice’s maxims fall under my notion of soft mathematics. Grice made successful use of his maxims in analyzing a widespread conversational phenomenon he called “conversational implicature”. This is when a person says one thing and means something other than the literal meaning.

For example, suppose Naomi says to Melissa, “I am cold” after Melissa has just entered the room and left the door wide open. Literally, Naomi has simply informed Melissa of her body temperature. But what she means—or what she probably means—is “Please close the door.” Naomi’s words do not actually say this; rather it is implicated by her words.

Grice used the word “implicate” rather than “imply” for such cases since Naomi’s words certainly do not imply the “close the door” meaning in any logical sense. Assuming Melissa understands Naomi’s remark as a request to close the door, she does so because of cultural knowledge, not logic.

Conversational implicatures

Conversational implicatures are ubiquitous in our everyday use of language. They can be intended by the speaker, or can be made by the listener. Grice used his maxims to analyze the phenomenon. Let’s take a look at his analysis.

Suppose Mark meets Naomi and says,”How is the car your brother lent you?” Naomi replies, “Well, it hasn’t broken down so far.”

Mark’s question seems straightforward enough. What about Naomi’s reply? Assuming both Mark and Naomi are obeying Grice’s Cooperative Principle, that is to say, they are engaged in a genuine attempt to have a conversation, and not trying to mislead each other, what are we to make of Naomi’s words? Presumably Naomi is implying, in a roundabout way, that she does not expect her brother’s car to be in good order. She is implicating this unspoken meaning. Most people in Mark’s position would probably take Naomi’s reply that way. But what is the logic behind this particular use of language? After all, Naomi certainly does not come out and say “My brother’s car is likely to be unreliable.”

In terms of the maxims, here is a Gricean analysis of the Mark and Naomi example. On hearing Naomi’s reply, Mark could reason as follows:

Naomi’s remark appears to violate the maxim “Be perspicuous.”
On the other hand, I have no reason to suppose she is opting out of the Cooperative Principle.
Given the circumstances, I can regard the irrelevance of Naomi’s remark as appropriate if, and only if, I suppose she thinks her brother’s car would be likely to break down.
Naomi knows I am capable of working out that last step.
Thus Naomi is implicating that her brother’s car would be likely to break down.

Of course, few if any of us would actually go through such a reasoning process. But that is not the point. In a similar vein, people rarely consult the axioms of logic when putting forward a logical argument, but that does not prevent a logician from analyzing their argument and checking to see if is valid by seeing if it accords with the rules of logic.

Though scientists like to understand how something “really” is, they often settle for a plausible explanation of the phenomenon that fits the known facts. In explanations of human activities such as reasoning and conversing, one way to see if a particular explanation fits the facts is to see if it would provide a reasonable response to a challenge of “How did you reach that conclusion?” In the case of Mark and Naomi’s conversation, imagine a bystander asks Mark what he understood by Naomi’s concluding remark, and to explain how he reached that conclusion. Most people in Mark’s position would probably respond with an explanation something like the one just given, though perhaps much shorter and, unless they knew about Grice’s maxims, not using his technical terminology.

Though Grice makes no claim that people have any conscious awareness of his maxims, his discussion of conversational implicature establishes a strong case that the maxims capture part of the abstract structure of conversation. They do after all enable the linguist to provide satisfactory, after-the-event explanations of a variety of conversational gambits.

According to Grice, a participant in a conversation, say Bill in conversation with Doris, may fail to fulfill a maxim in various ways, including the following.

(1) Bill may quietly and unostentatiously violate a maxim. In some cases, Bill will thereby mislead Doris.

(2) Bill may opt out from the operation both of the maxim and the Cooperative Principle, making it plain that he is unwilling to cooperate in the way the maxim requires. For example, he might say, “I cannot say more. My lips are sealed.”

(3) Bill may be faced with a clash. For example, he may find it impossible to satisfy both the quantity maxim “Be as informative as required” and the quality maxim “Have adequate evidence for what you say.”

(4) Bill may flout or blatantly fail to fulfill a maxim. Assuming that Bill could satisfy the maxim without violating another maxim, that he is not opting out, and that his failure to satisfy the maxim is so blatant that it is clear he is not trying to mislead, then Doris has to find a way to reconcile what Bill actually says with the assumption that he is observing the Cooperative Principle.

Case (4) is the one that Grice suggests most typically gives rise to a conversational implicature.

Let’s take a look at some more examples of everyday conversational implicatures.

For some implicatures, no maxim is violated. For example, suppose Roger drives up to a policewoman and says, “I’m almost out of gas,” and the policewoman replies, “There’s a gas station around the corner.” By the maxim “Be relevant,” Roger can infer that the gas station is open.

In contrast to the gas station scenario, the next example involves apparent violation of the “Be relevant” maxim in a very clear way in order to produce the intended implicature.

Arthur says, “Bill doesn’t seem to have a girl friend these days.” Susan replies, “He has been spending a lot of time in Denver lately.” Susan’s response will violate the “Be relevant” maxim unless she intends her reply to implicate the fact that Bill has, or at least she suspects that he has, a girlfriend in Denver, and she wants her remark to suggest that that is the reason for his frequent visits there.

For another kind of example, suppose Greg has been telling Melissa of his intention to visit Europe, and has mentioned that he would like to visit her friend Yannis. He asks, “Where does Yannis live?” and Melissa replies, “Somewhere in Greece.” Clearly, Greg was asking for the name of the location where Yannis lives, in order to see if it would be possible to visit him. Hence Melissa’s reply violates the quantity maxim “Make your contribution as informative as is required.” Assuming that Melissa is not violating the Cooperative Principle, the conclusion Greg can draw is that Melissa violates the quantity maxim because to say more would require that she violates the quality maxim “Do not say that for which you lack adequate evidence.” In other words, Greg concludes that Melissa does not know the city or town where Yannis lives. Indeed, assuming Melissa is being as informative as she can, Greg may conclude that Melissa cannot be more specific than she has.

People sometimes flout maxims in order to achieve by implicature an information exchange they would, for some reason, prefer not to state explicitly. For example, suppose Professor Alice Smith is writing a testimonial for her linguistics student Mark Jones, who is seeking an appointment at a university. She writes a letter in which she praises Jones’s well groomed appearance, his punctuality, his handwriting, and his prowess at tennis, but does not say anything about his ability as a student. Clearly, Professor Smith is flouting the quantity maxim “Make your contribution as informative as is required.” The implicature is that Professor Smith has nothing good to say about Jones’s academic ability, but is reluctant to put her opinion in writing.

Irony is often achieved by a violation of the quality maxim “Do not say what you believe to be false.” For example, suppose Jane has been telling Richard how badly her friend Sally had let her down, and Richard comments, “Well, Sally certainly is a great friend.” The implicature is that Sally is a very poor friend.

Metaphor is another linguistic affect that may be achieved by flouting the same quality maxim. For example, if Tom says to his wife, “You are the cream in my coffee,” the implicature is that Tom thinks his wife is the completion to his life.

Violation of the quality maxim “Do not say what you believe to be false” may also be used to achieve the effect of understatement. An example of this is where Barbara and George have had an enormous fight, in which Barbara ended up flinging crockery all over the kitchen, and the next morning Barbara approaches George and says, “I was a bit annoyed last night.” The implicature is that Barbara was, as George knows full well, thundering mad. In this case, George probably takes her words as an acknowledgement of, or even an apology for, her behavior.

So far, none of the examples have involved the maxims of manner. Here are three that do.

Parents of young children sometimes flout the manner maxim “Avoid obscurity of expression” in order to communicate with each other in a manner that their children cannot comprehend, saying things like “Did you pick up the you-know-what on your way home?”

Politicians sometimes try to violate the “Avoid ambiguity” manner maxim in order to mislead their audience.

Neither of the above two examples results in an implicature. However, suppose John says to Sally, “Mary produced a series of sounds on the piano that sounded like ‘Home on the Range’.” This violates the manner maxim “Be brief,” and the implicature is clearly that Mary’s piano playing was not very good.

The above examples illustrate that way a person can make (implicit) use of Grice’s maxims to convey a meaning other than the literal meaning of the words actually spoken. The maxims provide some of the “logic” of conversation, just as Aristotle’s syllogisms provided some of the “logic” of reasoning.

Is Grice’s work mathematics? Clearly not. (Hence his work does not constitute mathematical modeling.) Is it inspired by, and modeled on, the mathematical approach. You bet your life it is.

NOTE: Grice’s original essay is widely available on the Web as a PDF file.

Devlin’s Angle is updated at the beginning of each month.

Mathematician Keith Devlin (email: devlin@stanford.edu) is the Executive Director of the Human-Sciences and Technologies Advanced Research Institute (H-STAR) at Stanford University and The Math Guy on NPR’s Weekend Edition. His most recent book for a general reader is The Unfinished Game: Pascal, Fermat, and the Seventeenth-Century Letter that Made the World Modern, published by Basic Books.

NOVEMBER 2009

Cross Talk

My title is intentionally ambiguous.

I sometimes think that the very precision of mathematics that gives it much of its power can lead to problems when it comes to mathematics education in the lower school grades. I was reminded of this recently when both sides of a debate about mathematics standards emailed me about a particular issue.

The point of contention was a statement that pupils should be aware of the relationship between perimeter and area of plane figures.

From a strictly mathematical perspective, there is of course no relation between perimeter (meaning the length of the perimeter) and the area (that is, the numerical figure we ascribe as a measure of an enclosed plane region). A given perimeter length can enclose a whole range of different areas, going down as close to zero as you choose and up to a maximum determined by the kind of figure you wish to construct (rectangles, rectilinear, ellipses, etc.) As a reader of MAA Online, you know that, so do I, and so did the two antagonists who wrote to me.

But then, we all learned about lengths and areas many years ago, and the concepts are familiar to us. Things seem very different to someone learning mathematics for the first time. Recently I had occasion to talk with some researchers who had worked with several classes of young learners using a neat little computer tool that allowed them to use a given length of “perimeter-wire” in order to enclose rectilinear fields (of the farming variety) of several given target areas. Except for the case when the target area could be achieved with a rectangle, the students found it immensely difficult, and in many cases impossible without assistance. This known difficulty was, of course, the point of the activity!

Using the tool, the students were able to experiment with the way different rectilinear configurations of the same overall length produced enclosed regions with different numerical areas. In a variant, given a target area, they had to select the perimeter length from a given menu. How else would you describe the activity? I would say they were investigating the relationship between perimeter and area. Indeed, I suspect they came out of the exercise having recognized that perimeter (both shape and length) and area (both shape and numerical measure) are related. Change one factor and the others change too.

So which of my two correspondents was correct? The answer was they both were. At issue was the perspective from which they were approaching the issue: formal mathematical as understood by a mathematician, or cognitive-conceptual in the elementary or middle school classroom.

In writing state standards, which is what occasioned the debate into which I ever-so-briefly injected my two-cents worth, it is surely important to find terminology that captures both perspectives. As I have argued previously in this column, while it is educationally crucial that we understand the way new material will appear to someone learning it for the first time, and design our instruction accordingly, we should not proceed in a fashion that leads them to adopt incorrect concepts or form false mental models, that must later be undone. (Not least because the evidence is clear that in many cases no amount of subsequent “corrective instruction” can eliminate a first-acquired, false notion.)

Those of us in mathematics need to be aware that our love of precision, so important within the discipline, can cause problems if taken blindly into the school classroom. Definitions matter. Words matter. The words we use as mathematicians have other meanings too. Knowing how to bridge the two cultures and their two linguistic usages is part of being a good mathematics teacher.

Devlin’s Angle is updated at the beginning of each month.

Mathematician Keith Devlin (email: devlin@stanford.edu) is the Executive Director of the Human-Sciences and Technologies Advanced Research Institute (H-STAR) at Stanford University and The Math Guy on NPR’s Weekend Edition. Devlin’s most recent book for a general reader is The Unfinished Game: Pascal, Fermat, and the Seventeenth-Century Letter that Made the World Modern, published by Basic Books.

DECEMBER 2009

Strictly for the birds

With Christmas almost upon us, I thought I’d use this month’s column to give you two of my favorite brain-teasers to challenge your relatives at that family gathering. What I like about these problems is that when you first meet them, you think you don’t have enough information to solve them. But you do. You just have to look carefully at what the problem says. Both puzzles are about birds. I don’t know the origin of the first one, but the second has a famous history.

Bird puzzle 1

A new assistant accidentally left open the cages at the pet shop, and over 100 birds escaped. There were exactly 300 birds to begin with. The next morning, the local newspaper carried a report that gave the following figures:

“Of the birds that remained, a third were finches, a quarter were budgies, a fifth were canaries, a seventh were mynah birds, and a ninth were parrots.”

However, the reporter got one of the fractions wrong. How any parrots were left?

Bird puzzle 2

The second puzzle appears in the famous book Liber abbaci, published in 1228 by Leonardo of Pisa, known today as Fibonacci. It is sometimes referred to as “Fibonacc’s problem of the birds.” I’ll state it by copying verbatim from the English language translation of Leonardo’s great work by Laurence Sigler (Springer-Verlag, 2002), who until his death in 1997 was a Professor of Mathematics at Bucknell University. (The “denaro” was a unit of currency in Medieval Italy.)

A certain man buys 30 birds which are partridges, pigeons, and sparrows, for 30 denari. A partridge he buys for 3 denari, a pigeon for 2 denari, and 2 sparrows for 1 denaro, namely 1 sparrow for 1/2 denaro. It is sought how many birds he buys of each kind.

As before, what makes this problem particularly intriguing is that it seems you don’t have enough information to solve it. Specifically, it looks like you have two equations in three unknowns. In fact, in terms of equations, that is precisely what you do have. But the problem gives you additional information that turns out to be all you need to find the (unique) answer.

I’ll give the answers to both puzzles in next month’s column.

Devlin’s Angle is updated at the beginning of each month.

Mathematician Keith Devlin (email: devlin@stanford.edu) is the Executive Director of the Human-Sciences and Technologies Advanced Research Institute (H-STAR) at Stanford University and The Math Guy on NPR’s Weekend Edition. His most recent book for a general reader is The Unfinished Game: Pascal, Fermat, and the Seventeenth-Century Letter that Made the World Modern, published by Basic Books.