2010 POSTS

JANUARY 2010

Repeated addition—one more spin

If you came here to find the answers to the puzzles I gave in last month’s column, you’ll find them further down the page.

Talking of the new year, why do mathematicians think that this is an ideal year?

I’ll answer that teaser next month.

First up for 2010, however, I want to return, briefly, to a topic I covered extensively in this column in 2008. Namely, the clear distinction—long recognized by mathematicians, and much emphasized by leading mathematics education scholars going back to Piaget, and in at least one leading industrial country (Japan) mandated for teachers to respect—between multiplication and repeated addition. (For newcomers, I’ll begin by saying it one more time: multiplication is not, repeat not, repeated addition. Not even for positive whole numbers. This is the one case where you do get the same answer, but getting the same answer to two procedures does not make them the same procedure.)

You’ll find the story so far in Devlin’s Angle for June 2008, July 2008, and September 2008, with related articles in December 2008 and January 2009.

The series generated a huge response in my email inbox and on the blogosphere. Some of it applauded me for creating greater awareness of several hundred years of advances in mathematics and over sixty years of research in mathematical education that had somehow failed to migrate into the everyday educational world. In contrast, a lot of it amounted to little more than people calling me an idiot or a crank and repeating, Canute-like, the mantra “Multiplication is repeated addition” over and over again. All very edifying and scientifically convincing, I must say.

After three columns, with the final one in September 2008 being a long piece citing some of the scholarly research on which I based my articles, and then the two somewhat related follow-up pieces, I felt it was time to put the topic to bed as far as my involvement was concerned. But thanks to search engine technology, from time to time someone comes across my articles and writes to me about the issue.

One question that comes up frequently generally goes like this. “Sure, the repeated addition definition doesn’t work for multiplying fractions, let alone irrational numbers, but can it cause later problems if multiplication of positive whole numbers is introduced (to young children learning math) as repeated addition?” Now, some of the research I cited in my September 2008 column indicates that it certainly can. But the issue comes up sufficiently often that I wish I had given just one more example in my originals articles. Here it is.

For those who claim that multiplication of positive whole numbers really is just repeated addition, let me ask you how you would explain to a small child the mathematics that describes this simple activity.

Take a piece of elastic, and tie two knots in it, one near each end. Ask the child to measure the distance between the knots. Suppose it turns out to be 5 inches. Now, as the child watches, slowly stretch the elastic until the distance between the two knots is 10 inches. Get the child to measure it again. Now ask the child to write down a mathematical description of how the new length depends on (is related to) the original length. I would hope the child writes down

10 = 2 x 5

In more general terms, what you did was double the length, or, as an equation:

new length = 2 x old length

I would be very surprised if the child wrote down

10 = 5 + 5

corresponding to

new length = old length + old length

and if he or she did, you would have your work cut out trying to put them right before they have serious trouble in the math class. Sure, these addition equations are numerically correct. But so what? What you have just shown the child when you stretched the elastic has absolutely nothing to do with addition and everything to do with multiplication.

Wikipedia actually gets it right (at least it did when I checked on January 1 at 2:00 PM PST) when it says:

Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic (the others being addition, subtraction and division).

Unfortunately, it then immediately gets it wrong by going on to say, “Multiplication is defined for whole numbers in terms of repeated addition”, which is totally at odds with the first statement, and an illustration of the dangers of the wisdom of the crowds approach behind Wikipedia. (Saying “can be defined” is a bit better—and historically correct if you go back a thousand years or more—but, as the research shows, it’s unfair to the child to present it that way, since it will likely cause problems later. Besides being flat wrong. Multiplication is not defined in that way, and has not been for centuries. As Wikipedia’s first statement says, multiplication is a basic arithmetic operation; as such, it is not defined in terms of anything else.)

ASIDE: Actually, as a factual observation about the world we live in, at least in our cocoon-like United States, that second part of the Wikipedia entry (the “multiplication is defined” statement) is all too frequently distressingly correct: it often is defined that way. If you want to bring the repeated addition connection in to the multiplication scene (and it surely makes good educational sense to bring it in pretty soon, or even better guide the kids to discover it for themselves), then the correct statement is that, “Multiplication gives you a fast, efficient way to calculate the answer to a repeated addition sum.” (Saying it the other way round is inexcusable. Repeated addition is most definitely not an efficient way to do multiplication. If you don’t believe me, let’s have a timed competition to multiply 1,000 by 999.

Still, for all its failures, Wikipedia is somewhat better than many of the other websites you come up with when you google “multiplication”, not least one by an education services entrepreneur who is savvy enough to name his company in a way that will likely get his product at or near the top of your search (full marks for that, Sir), but whose product gets multiplication flat wrong from the getgo, and who may be setting himself up for a class-action lawsuit when users of his product subsequently find themselves with real problems in math due to such a misleading start.

Okay, enough of that. Now for the answers to last month’s puzzles.

Answers for the birds

In my December, Christmas Special column, I left you with the following two puzzles:

Bird puzzle1

A new assistant accidentally left open the cages at the pet shop, and over 100 birds escaped. There were exactly 300 birds to begin with. The next morning, the local newspaper carried a report that gave the following figures:

“Of the birds that remained, a third were finches, a quarter were budgies, a fifth were canaries, a seventh were mynah birds, and a ninth were parrots.

However, the reporter got one of the fractions wrong. How any parrots were left?

Bird puzzle 2

Fibonacci’s problem of the birds: A man buys 30 birds, a mixture of partridges, pigeons, and sparrows, for 30 denari. A partridge costs 3 denari, a pigeon 2 denari, and a sparrow 1/2 denaro. How many birds of each kind does he buy?

This problem comes from Fibonacci’s Liber abbaci, published in 1228 (the surviving second edition), the book that brought breeding rabbits and Hindu-Arabic numbers to western Europe. The “denaro” was a unit of medieval currency.

The answers

What makes both problems particularly intriguing is that in each case it seems you don’t have enough information to solve it. But in fact you do. Here are the answers.

Let R be the number of birds that remained in total, and let F, B, C, M, P be the number of finches, budgies, canaries, mynah birds, and parrots that were left. Suppose the reporter had got all the facts correct. Then we would have:

F = R/3, B = R/4, C = R/5, M = R/7, P = R/9

So,

R = 3F, R = 4B, R = 5C, R = 7M, R = 9P

If correct, these five equations tell us that R is a common multiple of 3, 4, 5, 7, 9.

So R is at least 4 x 5 x 7 x 9 = 1260.

But we know the reporter got one fraction wrong. Thus the most we can know is that R is a common multiple of four of the numbers 3, 4, 5, 7, 9.

What are the possibilities?

The common multiple of 3, 4, 5, 7 is 420; that of 3, 4, 5, 9 is 180; for 3, 4, 7, 9 it is 252; for 3, 5, 7, 9 it’s 315; and for 4, 5, 7, 9 you get 1260.

Thus, depending on which number the reporter got wrong, we can conclude that R is at least 420, 180, 252, 315, 1260, respectively.

There were exactly 300 birds at the start, and over 100 birds escaped. So the number of the birds that remained is less than 200.

Of the different possible minima for R, only 180 is less than 200. So R has to be 180. (In order words, the reporter got the fraction of minah birds wrong.)

So the number of parrots that stayed is 180/9 = 20.

DRUMROLL!

So much for the first puzzle. What about Fibonacci’s teaser?

Let x be the number of partridges, y the number of pigeons, and z the number of sparrows. Then the information you are given leads to two equations:

x + y + z = 30 (the number of birds bought equals 30)

3x + 2y + z/2 = 30 (the total price paid equals 30)

Hmmm. As everyone learns in the high-school algebra class, you need three equations to find three unknowns. So what to do next?

Well, in this case you have one crucial additional piece of information that enables you to solve the problem. First, double every term in the second equation to get rid of that fraction:

x + y + z = 30

6x + 4y + z = 60

Subtract the first equation from the second to eliminate z:

5x + 3y = 30

Notice that 5 divides the first term and the third, so it must also divide y. So y is one of 5, 10, 15, etc.

But y cannot be 10 or anything bigger, since then it could not satisfy that last equation!

Thus y = 5. It follows that x = 3 and z = 22. Neat, eh?

Devlin’s Angle is updated at the beginning of each month.

Mathematician Keith Devlin (email: devlin@stanford.edu) is the Executive Director of the Human-Sciences and Technologies Advanced Research Institute (H-STAR) at Stanford University and The Math Guy on NPR’s Weekend Edition. His most recent book for a general reader is The Unfinished Game: Pascal, Fermat, and the Seventeenth-Century Letter that Made the World Modern, published by Basic Books.

FEBRUARY 2010

Is math a socialist plot?

Last month, on the most recent of my occasional appearances on NPR as the Math Guy, I talked about a formula developed by a British mathematician to determine the minimum space required between parked cars in order that you can park your car between them with a simple one-two, reverse-in-and-drive-forward maneuver. You can listen to the piece, and read about it here.

You can also read the mathematical paper that led to the story, by Professor Simon Blackburn of Royal Holloway University, London.

The NPR website also has the listeners’ discussion thread generated by the program. This is what I want to talk about today. Glancing at it a few hours after the program aired, I noticed something of interest regarding the popular conception of mathematics. So much so, that on a couple of occasions I threw in a response myself, to try to dig a bit deeper.

The result is, of course, hardly a scientific survey. The total number of contributions was only 69, including repeat submissions by some listeners. On the other hand, the contributors were individuals who (1) prefer to get their news, or at least some of it, from NPR, and (2) are sufficiently interested in a story about mathematics to take the time to sit down at a computer and write in a comment.

Apropos my mention of NPR listeners, I note that the NPR audience is about a mere 8% of the U.S. population, and is significantly more educated than the population as a whole. Which is why I think it is worth taking at least some account of the responses to my parking piece.

Over-educated? A brief aside

Talking of the educational level of NPR listeners—and now I may appear to be straying slightly off my main topic, but as you will see this ties in with the thrust of this month’s column, namely national education standards and U.S. economic competitiveness—did anyone else notice the article on Yahoo! News on January 29, written by Sam Stein, which carried the headline “Obama Still Loved by the Over-Educated”?

“Over-educated”? I did a double-take. Is it ever the case that a person can have too much education? Surely it’s a misprint. No, there it is again in the article’s very first sentence,

“President Obama’s popularity has slipped among a wide swath of the population. Among the nation’s overeducated, however, he continues to do just fine.”

Good Lord. What can Mr. Stein possibly mean? Our reporter goes on to say,

“Gallup surveyed more than 25,000 voters over the past calendar year and found that the president remains well-liked among those with multiple degrees.”

Ah, there we have it. According to Mr. Stein, and the editors at Yahoo! News who published his educational wisdom, anything beyond a bachelors degree amounts to over-education. Not so Gallup, I’m relieved to say. The research organization itself published the result of its survey under the deadline “Americans With Postgraduate Education Still Back Obama”. No, it’s Mr Stein and his editors at Yahoo! News that think anything beyond a first degree amounts to over-education.

Folks, if the (presumably under-educated, or so he comes across) Mr. Stein is at all representative of the U.S. population, and it is indeed generally believed that anything beyond a bachelors degree is superfluous, then we may as well just throw in the towel when it comes to international competitiveness and start to learn Chinese and Hindi. I only hope for his sake that Mr. Stein never gets sick. He’s going to have a devil of a time trying to find a physician who is not over-educated. And we can assume he never uses Google in his research, right? That, after all, came right out of a post-graduate research project at Stanford—you know, the superfluous stuff we don’t really need.

Enough of this anti-educational ignoramus rant. What about parking?

I first came across Professor Blackburn’s car parking formula from an MAA News Alert. “Aha!” I thought. “This might make a nice piece for the Math Guy to talk about on Weekend Edition.” I knew that a story that links math and car parking was sure to grab listeners’ attention.

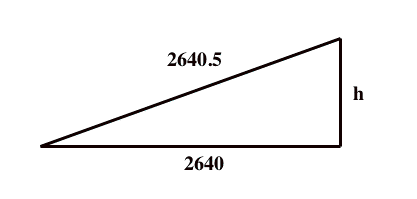
A quick Google search (gosh, wasn’t life much better before we were over-educating all those people like the Google founders?) took me to Blackburn’s university homepage, along with his paper. The mathematics he used turns out to involve nothing beyond Pythagoras’ Theorem. Strike two! I would not have to tell listeners, as I often have to, that “the math is pretty complicated, and can be understood only by people with a Ph.D. in math.” True, Blackburn has to use Pythagoras’ Theorem in a way that is a bit more complicated than many high school students are used to seeing, but nothing that a good high school student could not follow—or even work out for themselves.

So now I have a story with an attractive audience hook where the math is something everyone saw at school. The one other thing you need to make a science news story work is to be able to answer the question “What is this good for?”

Why this is an important question, has always baffled me. After all, the news media are full of reports about sports, music, movies, entertainment, and the arts, none of which are “good for anything” in the sense that science stories are supposed to live up to. “People enjoy it” or “Entertainment is a good thing in itself” or even “People are just naturally curious and want to know stuff” (though not too much according to Mr. Stein) are generally regarded as sufficient justification for most things the news media report on.

Still, my colleagues in the media tell me that a science story won’t work unless it gives an indication of a possible “application”. And I know from many years of experience that, as in any other profession, the professionals in this case do know what they are talking about. (The story I am about to tell you provides further confirmation of the science-story-application dictum.)

Who needs a math formula for parking?

Professor Blackburn states on his webpage that his research into the mathematics of parking had been commissioned by, and paid for by, Vauxhall Motors, a division of General Motors. Now, Vauxhall did not say why they asked the professor to develop a mathematical formula for parking cars. On the other hand, they did make it clear that they now own the formula he came up with, so we can assume they think it may have commercial value to them.

My own immediate reaction when I first came across the story on the MAA website was that they were planning on developing an automated parking control system. Toyota introduced a commercial automatic parallel parking system for the Prius way back in 2004, and similar systems have since been developed by Lexus, BMW, Volkswagen, and Ford. With the basics of reliable automotive engineering long since established, future competition between the remaining automobile manufacturers is likely to focus on the various extras they can offer. An automatic parking system was surely Vauxhall’s motivation.

Like almost everything else in the hugely competitive, automobile industry, the design details of automated driving aids such as parking systems are closely guarded trade secrets. But it doesn’t take a genius to realize that the first thing the system would need to know is whether there is enough space to even start the maneuver! People do that by experience. We become familiar with our car, and it’s usually enough to eyeball the available space in order to determine whether to go ahead and park there or look for somewhere else. An automatic parking system could use sensors to determine the dimensions of the space (length and width are both important), but how would it decide whether that space is enough?

“An on-board computer could do that,” I hear you cry. Indeed it could. Everyone now has grown used to the fact that computers can make simple decisions. What many people evidently do not know, however, is that they do so using mathematics, and thus they can do so only after the question has been converted into mathematical form. Give an automobile control system Professor Blackburn’s formula (or else a table of values computed in advance from the formula) and it will be in business. (There are other approaches. But the simplest, cheapest, and almost always the most reliable, is the mathematical formula approach. In fact, the other approaches all involve mathematics in one way or another, though perhaps not in the form of a single formula embodied in a computer program.)

So, although I could not say to my NPR listeners with certainty that Vauxhall wanted the parking formula in order to build an automatic parking system, I could address the application issue by saying I was pretty sure that was the case. I had my story.

What is math for?

The recording went well. (Everything you hear on Weekend Edition is recorded in advance except for the weekly interview with Daniel Schorr.) It was, we all felt, a fun as well as informative piece. It also met an additional requirement I always strive for but often cannot meet, which is to provide an example of how mathematics is discovered and used that teachers could take into their classes on Monday morning.

In this case, it hit that goal in spectacular fashion, since the math was school level and the application was so obvious and self-evidently relevant both to our everyday lives and to the prosperity of the nation (or at least to General Motors, whose fortunes are perhaps no longer quite the same as those of the United States, but are still important to us all).

As often happens, when Saturday morning rolled around and the day’s news came in, my parking segment had to be cut down, so the bit about the possible application of the new formula was not included in the piece that was broadcast. Doubtless the producer (decidedly not a math person) felt, as I did when I heard the piece over the air, that for this story at least, the application was blindingly obvious. Well, it turns out that to some listeners, it was not at all clear what the application was. (And remember we are talking about “well-“, if not “over-educated”, NPR listeners, who are interested in a math story.)

Actually, that is not quite true. They did think they knew what the application was. And that, I fear, tells those of us in mathematics education the impression many of our students have when they leave us. Several respondents said things along the lines of “I don’t need a math formula to tell me how to park,” or “No one has the time to acquire and plug the numbers in and do that calculation before they park.” In other words, when they see a formula, they think the purpose is to put numbers into it and work out the answer.

Who is to blame?

Where on earth do they get that idea? I’ll tell you where. From all those exercises in school math textbooks that present mathematics in exactly that way. Even worse, those textbooks do so under the pretext that this shows the students “real life applications of math.”

You know the type of problem, finding out how long it takes a swimming pool to fill from a hose that delivers X gallons of water a minute, or how much concrete you need to order to lay a driveway Y feet by Z feet by H feet deep. The textbook or the teacher may say that this shows why the math is useful, but the student knows full well it does nothing of the kind, and so, I suspect, do the textbook author and the teacher in most cases.

Faced with filling a swimming pool with water, what you, and I, and everyone on the planet would do, is turn on the water, watch for a minute or two to get a sense how fast the water level seems to rise, then do something else nearby, checking periodically on the progress until it’s getting close to being full, and then watching it until it’s done. And although I once did meet a math teacher who swore she actually did calculate the amount of concrete required to lay a driveway at her home, I suspect most people would call in a contractor who would come to the site, pace out the dimensions, and then take advantage of years of experience to say, “This will take one and a half truckloads. Tell me if there’s anything else you want me to do with any that’s left over.”

In the real world in which real people live, even the mathematically over-educated, no one uses mathematical formulas in their day-to-day life. In their work, perhaps. But not in the daily stuff of living. What they often do find themselves doing is using a device or a smartphone app or an automobile dashboard display that depends on math. This is so common that it’s not at all difficult to show students where and how math is used. Our students, and we, are surrounded by such examples. Why, oh why, resort to fake “applied problems” when there are plenty of real ones? The only difference with past eras is that, these days, it’s not people who “do the math,” it’s the various devices we buy, use, and carry around with us. And as the parking formula shows, those genuine applications can sometimes involve very basic math.

Even in the case where you can’t find a genuine application of some mathematics, it’s not hard to imagine a plausible one. Instead of asking students to carry out the swimming pool example with an unrealistic scenario, say that their boss wants them to develop a small automatic valve that can be set to turn off the water when the pool is full, or that a local builder has asked them to develop a smartphone app or a website calculator that customers can use to determine how much concrete they need when placing their order. These are formulations that will seem relevant to the students. The students will, of course, end up doing the same math! You’re just presenting it in a plausible fashion.

BTW, I’m not arguing against people learning how to solve math problems. There are several good reason why solving math problems is a valuable part of education. One is that time spent solving math problems develops analytic thinking skills that prove beneficial in other walks of life. But that reason does not work well with young people who have not yet had time to experience the benefits. (It doesn’t work so well with lots of others either, though in my experience people who say “I never could do math but I did okay for myself” often go on to say something that demonstrates they, or at least those who have to put up with their ill-thought-out pronouncements or decisions, would likely have benefited tremendously from their having put a bit more effort into the math class.)

What I am saying is, please don’t use unrealistic, fake scenarios and tell the students they are seeing “How math is really used.” Give them realistic examples. Plainly, many of the contributors to the NPR discussion following my piece simply had no idea that mathematics was required in order to develop computer control systems. They saw a math formula and thought that we—that would be me and NPR—were implicitly claiming that it’s purpose was for a human driver to calculate whether there was enough space to park. Sheesh. Give me a break.

In fact some contributors went on to say they thought the research that led to the formula was a waste of time. Just think about that for a moment. Regardless of whether this particular formula is ever used in an automatic parking system, research into the topic is clearly critical to the competitiveness of the U.S, automobile industry. Haven’t we had out butts kicked too many times in that industry to think that research into ways of remaining competitive is a waste of time? What about other uses of the same kind of research, such as building robots that U.S. troops in Afghanistan and Iraq can use to search buildings for explosive devices? Is saving the lives of troops a waste of time? I could go on, but surely I’ve made my point.

Now I am pretty sure that not one of the NPR discussion contributors would say making our industries competitive or saving the lives of U.S. troops was a waste of time. They effectively made those claims because they have absolutely no idea how mathematics is used in today’s world. Moreover, they have formed this belief after having had at least ten years of almost daily mathematics instruction. In fact, so firmly rooted is their belief that math is something you do at school to solve irrelevant problems but is of no use in the real world, that even when I jumped into the online discussion and explicitly gave some examples (the ones in the above paragraphs), they remained unable to see math in a new light.

Forget whether they came out of the school system good at math or hopeless at it. I’m not talking about how good or bad they are at doing it. They don’t even know what it is or what it is used for. For comparison, I don’t know in much depth how an airplane flies, and I could neither fly one nor build one, but I have somehow managed to learn what it is and what it is used for. That’s all I’m talking about for mathematics, for heavens sake! When ten or more years instruction fails to leave people having even the faintest idea what something is, why it is done, or what it is used for, then something is seriously wrong.

Your homework for tonight is to find out what.

So what about the link between math and socialism?

Ah yes, my title promised something about mathematics being a socialist plot. What was that about? Well, two contributors to the NPR discussion claimed that this whole math thing was just a socialist plot. Since they provided no support for this assertion, I am inclined to give mathematics the benefit of the doubt here. More likely, I think, is that the two individuals habitually see everything as a socialist plot. Which is odd when you consider that by the definition of socialism implied by such individuals, Canada and every country in Europe would classify as socialist societies, though by and large those countries all seem pretty successful capitalist economies, and very definitely free societies with democratic governments. But I digress.

Okay, I admit, the socialist connection was a pretty small part of my essay, albeit an intriguing one. (It intrigued you, right?) My main reason for choosing the title I did was to try to ensure that you read through the entire column. Hey, if Channel 5 can promote the television evening news that way, why can’t I? If you did, and are still reading, my ploy was successful. I promise not to pull the same trick again—for a while. That Stein article really made my bristle.

Finally, the answer to last month’s quiz

Well, it wasn’t a quiz so much as a teaser. I asked why mathematicians think that this is an ideal year? The answer is that January 29 of this year marked the 200th anniversary of the birth of Ernst Eduard Kummer, who introduced the notion of an ideal. According to some accounts, he did so in 1843, when his attempt to prove Fermat’s Last Theorem broke down because the unique factorization of integers did not extend to other rings of complex numbers. According to that explanation, he attempted to restore the uniqueness of factorization by introducing “ideal” numbers. (He did of course prove Fermat’s Last Theorem for a large class of exponents.) Others, however, among them Harold Edwards, have stated that Kummer was motivated by his work on higher reciprocity laws. In any event, our modern notion of an ideal in a ring was introduced later by Richard Dedekind. Happy 200th birthday, Ernst Kummer.

Devlin’s Angle is updated at the beginning of each month.

MARCH 2010

The hidden math behind Alice in Wonderland

Promotional image for Tim Burton’s movie *Alice in Wonderland*, Walt Disney Pictures (2010)

Like James Cameron’s recent blockbuster movie Avatar, Tim Burton’s Alice in Wonderland, released this month, is in 3D. Also like Avatar, I suspect audiences will be uniformly thrilled with the visual spectacle, yet be divided when it comes to the story. Millions loved Cameron’s tale, but personally I (and apparently many others) thought that, although it had all the plot ingredients to have been good, it ended up annoyingly adolescent and cloyingly banal. As for Alice? Well, I’ll let you make up your own mind.

For mathematicians, the real story is not so much whether Burton’s movie will be a hit, rather it’s not often that a mathematical allegory makes it to Hollywood blockbuster status in the first place! So I can’t let the release of Alice go unnoticed in the mathematical literature—to whit Devlin’s Angle. For, as readers of MAA Online will doubtless know, Lewis Carroll was the pen name of the Reverend Charles Lutwidge Dodgson, a mathematician at Christ Church College, Oxford, and most mathematicians are probably aware that elements of the Alice story were inspired by mathematics. (At least, that is the entirely reasonable assumption everyone makes; Dodgson himself provided no commentary to that effect.)

Before I go any further, I should note that the new Alice movie is not based on Lewis Carroll’s original book. (Actually, the memories of the Alice story we all have from our childhood are based on two books, Alice in Wonderland and the later Alice Through the Looking Glass.) Rather, Burton takes as his inspiration a computer game called American McGee’s Alice. In the film, an adult Alice, now a disturbed young woman mourning the death of her parents, returns to the land we are familiar with from Carroll’s original tale, a strange place where animals talk, the Cheshire Cat has a grin, and the Queen of Hearts is wicked. (Or was it the Red Queen? Carroll’s two books had different queens that over the years tend to merge in our memories.)

Though others had looked for political and social allusions in the Alice books, most notably Clarkson Potter, whose The Annotated Alice was published in 1960, and Martin Gardner, whose sequel More Annotated Alice came out in 1990, perhaps the first scholar to look in depth for possible mathematical inspirations for Alice was Helena Pycior of the University of Wisconsin-Milwaukee, who in 1984 linked the trial of the Knave of Hearts with a Victorian book on algebra.

Now Melanie Bayley, of the University of Oxford in England, has taken the analysis a lot further. She described her findings (well, since we are in the realm of literary interpretation here, I’d better say “her theory”) in an article titled Alice’s adventures in algebra: Wonderland solved, published in New Scientist, 16 December 2009.

Before I relate what Bayley has to say, let me summarize the history of Carroll’s Alice in Wonderland

In 1862, Dodgson, together with the Reverend Robinson Duckworth, rowed in a boat up the River Thames with three young girls, Lorina Charlotte Liddell, aged 13, Alice Pleasance Liddell, aged 10, and Edith Mary Liddell, aged 8, the daughters of Henry George Liddell, the Vice-Chancellor of Oxford University and Dean of Christ Church College, as well as headmaster of the nearby, private, Westminster School.

The journey started at Folly Bridge near Oxford and ended five miles away in the village of Godstow. As they rowed, Dodgson made up and told the girls a story about a bored little girl named Alice who goes looking for an adventure. The three girls loved it, and Alice Liddell asked Dodgson to write it down for her. Two years later he did just that, and on 26 November 1864 he gave Alice the handwritten manuscript of what he then called “Alice’s Adventures Under Ground,” illustrated by his own drawings.

Most of the story was based on situations and buildings in Oxford and at Christ Church. For example, the “Rabbit Hole” down which Alice descends to begin her adventure symbolized the actual stairs in the back of the college’s main hall.

A year later, Dodgson—now masquerading as Lewis Carroll—published a greatly expanded version under the title “Alice’s Adventures in Wonderland,” with illustrations drawn by John Tenniel. It is in the new material he added, which includes the Cheshire Cat, the trial, the Duchess’s baby, and the Mad Hatter’s tea party, that we find allusions to mathematics. (Tweedledum, Tweedledee, Humpty Dumpty and the Jabberwock appear in the sequel, Alice Through the Looking-Glass.)

The book rapidly became a bestseller, it has never been out of print since it first appeared, and it has been translated into well over 100 languages.

So what does Bayley tell us about the mathematical ideas that Dodgson took inspiration from?

Now we get to the math part

First, we have to remind ourselves of what was going on in mathematics in the latter half of the nineteenth century, when Dodgson wrote his story. It was a turbulent period for mathematicians, with the subject rapidly becoming more abstract. The discoveries of non-Euclidean geometries, the development of abstract (symbolic) algebra that was not tied to arithmetic or geometry, and the growing acceptance—or at least use—of “imaginary numbers” were just some of the developments that shook the discipline to its core. By all accounts, Dodgson held a very traditionalist view of mathematics, rooted in the axiomatic approach of Euclid’s Elements. (He was not a research mathematician, rather he tutored the subject.) Bayley describes him as a “stubbornly conservative mathematician,” who was dismayed by what he saw as the declining standards of rigor. The new material Dodgson added to the Alice story for publication, she says, was a wicked satire on those new developments.

Perhaps the most obvious example is the Cheshire Cat, which disappears leaving only its grin, an obvious reference—critical in Dodgson’s case—to increasing abstraction in the discipline.

For a more focused example, take the chapter “Advice from a caterpillar.” Alice has fallen down the rabbit hole and eaten a cake that has shrunk her to a height of just 3 inches. The Caterpillar enters, smoking a hookah pipe, and shows Alice a mushroom that can restore her to her proper size. But one side of the mushroom stretches her neck, while another shrinks her torso, so she must eat exactly the right balance to regain her proper size and proportions. Bayley believes this expresses Dodgson’s view of the absurdity of symbolic algebra.

The first clue, she says, may be the pipe. The word “hookah” is of Arabic origin, like “algebra”. More to the point, the original Arabic term for algebra, widely known and used in the mathematical community in Dodgson’s time, was al jebr e al mokabala or “restoration and reduction”—which exactly describes Alice’s experience. Restoration was what brought Alice to the mushroom: she was looking for something to eat or drink to “grow to my right size again,” and reduction was what actually happened when she ate some: she shrank so rapidly that her chin hit her foot.

Bayley suggests that the overall madness of Wonderland reflects Dodgson’s views on the dangers of this new symbolic algebra. Alice has moved from a rational world to a land where even numbers behave erratically. In the hallway, she tries to remember her multiplication tables, but they have slipped out of the base-10 number system she is used to.

In the caterpillar scene, Alice’s height fluctuates between 9 feet and 3 inches. Alice, bound by conventional arithmetic where a quantity such as size should be constant, finds this troubling: “Being so many different sizes in a day is very confusing,” she complains. “It isn’t,” replies the Caterpillar, who lives in this absurd world.

The Caterpillar’s warning, at the end of this scene, is perhaps one of the most telling clues to Dodgson’s conservative mathematics, Bayley suggests. “Keep your temper,” he announces. Alice presumes he’s telling her not to get angry, but although he has been abrupt he has not been particularly irritable at this point, so it’s a somewhat puzzling thing to say. But the word “temper” has another meaning of “the proportion in which qualities are mingled.” So the Caterpillar could well be telling Alice to keep her body in proportion—no matter what her size. This may be another reflection of Dodgson’s love of Euclidean geometry, where absolute magnitude doesn’t matter: what’s important is the ratio of one length to another. To survive in Wonderland, Alice must act like a Euclidean geometer, keeping her ratios constant, even if her size changes.

Of course, she doesn’t. She swallows a piece of mushroom and her neck grows like a serpent with predictably chaotic results—until she balances her shape with a piece from the other side of the mushroom. This is an important precursor to the next chapter, “Pig and pepper”, where Dodgson parodies another type of geometry. By this point, Alice has returned to her proper size and shape, but she shrinks herself down to enter a small house. There she finds the Duchess in her kitchen nursing her baby, while her Cook adds too much pepper to the soup, making everyone sneeze except the Cheshire Cat. But when the Duchess gives the baby to Alice, it turns into a pig.

According to Bayley, the target of this scene is projective geometry, a subject that involved concepts that Dodgson would have found ridiculous, particularly the “principle of continuity.” Jean-Victor Poncelet, the French mathematician who set out the principle, described it as follows: “Let a figure be conceived to undergo a certain continuous variation, and let some general property concerning it be granted as true, so long as the variation is confined within certain limits; then the same property will belong to all the successive states of the figure.”

When Poncelet talked of “figures”, he meant geometric figures, of course, but Dodgson playfully subjects Poncelet’s description to strict logical analysis and takes it to its most extreme conclusion. He turns a baby into a pig through the principle of continuity. Importantly, the baby retains most of its original features, as any object going through a continuous transformation must. His limbs are still held out like a starfish, and he has a queer shape, turned-up nose and small eyes. Alice only realizes he has changed when his sneezes turn to grunts.

The baby’s discomfort with the whole process, and the Duchess’s unconcealed violence, signpost Dodgson’s virulent mistrust of “modern” projective geometry, Bayley says. Everyone in the pig and pepper scene is bad at doing their job. The Duchess is a bad aristocrat and an appallingly bad mother; the Cook is a bad cook who lets the kitchen fill with smoke, over-seasons the soup and eventually throws out her fire irons, pots and plates.

Alice, angry now at the strange turn of events, leaves the Duchess’s house and wanders into the Mad Hatter’s tea party. This, Bayley surmises, explores the work of the Irish mathematician William Rowan Hamilton, who died in 1865, just after Alice was published. Hamilton’s discovery of quaternions in 1843 was hailed as an important milestone in abstract algebra, since they allowed rotations to be calculated algebraically.

Just as complex numbers work with two terms, quaternions belong to a number system based on four terms. Hamilton spent years working with three terms—one for each dimension of space—but could only make them rotate in a plane. When he added the fourth, he got the three-dimensional rotation he was looking for, but he had trouble conceptualizing what this extra term meant. Like most Victorians, he assumed this term had to mean something, so in the preface to his Lectures on Quaternions of 1853 he added a footnote: “It seemed (and still seems) to me natural to connect this extra-spatial unit with the conception of time.”

As Bayley points out, the parallels between Hamilton’s mathematics and the Mad Hatter’s tea party are uncanny. Alice is now at a table with three strange characters: the Hatter, the March Hare and the Dormouse. The character Time, who has fallen out with the Hatter, is absent, and out of pique he won’t let the Hatter move the clocks past six.

Reading this scene with Hamilton’s ideas in mind, the members of the Hatter’s tea party represent three terms of a quaternion, in which the all-important fourth term, time, is missing. Without Time, we are told, the characters are stuck at the tea table, constantly moving round to find clean cups and saucers.

Their movement around the table is reminiscent of Hamilton’s early attempts to calculate motion, which was limited to rotatations in a plane before he added time to the mix. Even when Alice joins the party, she can’t stop the Hatter, the Hare and the Dormouse shuffling round the table, because she’s not an extra-spatial unit like Time.

The Hatter’s nonsensical riddle in this scene—”Why is a raven like a writing desk?”—may more specifically target the theory of pure time. In the realm of pure time, Hamilton claimed, cause and effect are no longer linked, and the madness of the Hatter’s unanswerable question may reflect this.

Alice’s ensuing attempt to solve the riddle pokes fun at another aspect of quaternions that Dodgson would have found absurd: their multiplication is non-commutative. Alice’s answers are equally non-commutative. When the Hare tells her to “say what she means”, she replies that she does, “at least I mean what I say—that’s the same thing”. “Not the same thing a bit!” says the Hatter. “Why, you might just as well say that ‘I see what I eat’ is the same thing as ‘I eat what I see’!”

When the scene ends, the Hatter and the Hare are trying to put the Dormouse into the teapot. This could be their route to freedom. If they could only lose him, they could exist independently, as a complex number with two terms. Still mad, according to Dodgson, but free from an endless rotation around the table.

The sting in the tale

Even if you accept Bayley’s suggestions—and obviously I am inclined to do so, at least overall, otherwise I would not have written about her work—you might think the mathematical inspirations for some of the scenes we read in Alice are nothing more than an interesting footnote. Think again, says Bayley. Without those mathematical undercurrents, it is highly unlikely that Dodgson’s book(s) would have achieved lasting, international stardom. His original nursery tale, written for the ten-year-old Alice Liddell, she says, would have been unlikely to attract much attention.

Dodgson was most witty when he was poking fun at something, Bayley explains, and then only when the subject matter got him truly riled. He wrote two uproariously funny pamphlets, fashioned in the style of mathematical proofs, which ridiculed changes at the University of Oxford. In comparison, other stories he wrote besides the Alice books were dull and moralistic.

“I would venture that without Dodgson’s fierce satire aimed at his colleagues,” Bayley claims, “Alice’s Adventures in Wonderland would never have become famous, and Lewis Carroll would not be remembered as the unrivaled master of nonsense fiction.”

Put that in your hookah and smoke it.

Devlin’s Angle is updated at the beginning of each month.

APRIL 2010

Probability can bite

Estimating probabilities can be a tricky business. The long running saga of the notorious Monty Hall Problem shows how even mathematically-smart people can easily be misled. (For my forays into that particular example, see my Devlin’s Angle columns for July-August 2003, November 2005, and December 2005.)

Another probability question that causes many people difficulty is the children’s gender puzzle: I tell you I have two children and that (at least) one of them is a boy, and ask you what you think is the probability that I have two boys. Many people, when they hear this puzzle for the first time, give the answer 1/2, reasoning that there is an equal likelihood that my other child is a boy or a girl. But this is not correct. Based on what you know, you should conclude that I am actually twice as likely to have a boy and a girl as I am to have two boys. So your right answer to my question is not 1/2 but 1/3

Before I explain the answer, I should clear up a confusion that many people have about problems such as this, which are about what is known as epistemic probability. The probability being discussed here is not some unchangable feature of the world, like the probability of throwing a double six with a pair of honest dice. After all, I have already had my two children, and their genders have long been determined. At issue is what probabilities you attach to your knowledg of my family. As is the case with most applications of probability theory outside the casinos, the probability here is a measure of an individual’s knowledge of the world, and different people can, and often do, attach different probabilities to the same event.

Moreover, as you acquire additional information about an event, the probability you attach to it can changes. To go back to the original puzzle now, in order of birth, there are four possible gender combinations for my children (ordered say, by birth): BB, GG, BG, GB. Each is equally likely. (To avoid niggling complications, I’m assuming each gender is equally likely at birth, and ignore the possibility of identical twins, etc.)

So, if all I told you was that I have two children, you would (if you are acting rationally) say that the probability I have two boys is 1/4. But I tell you something else: that at least one of my children is a boy. That eliminates the GG possibility. So now you know the possible gender combinations are BB, BG, GB.

Of these three possibilities, in two of them I have a boy and a girl, and in only one do I have two boys, so you should calculate the probability of my having two boys to be 1 out of 3, namely 1/3.

If you haven’t come across this before, it might take you some time to convince yourself this reasoning is correct. I long ago got past that stage, and hence felt my intuitions would be pretty reliable when I recently came across the following variant of the puzzle.

I tell you I have two children, and (at least) one of them is a boy born on a Tuesday. What probability should you assign to the event that I have two boys?

Before you read further, you should perhaps pause and try to figure this out for yourself

My initial reaction was that the information about the Tuesday was irrelevant, since at issue was gender, not day of birth. In which case, this was the same problem as the one I just described, and the answer would be 1/3.

But then I began to have second thoughts. I admit my doubts were occasioned by the way I came across the problem: a Twitter feed by the well-known mathematician John Allan Paulos, forwarding a tweet from the (British) Guardian newspaper science-writer Alex Bellos, who was reporting on the posing of this problem at the recent “Gathering for Gardner” conference in Atlanta by puzzle master Gary Foshee.

Suspecting that there was more to this problem than I initially thought, I set about repeating the same form of reasoning as in the original puzzle, but taking account of days of the week when my children could have been born. As soon as you do that, you realize that Foshee’s problem really is different. But how different? My intuition said that, since the original puzzle had the answer 1/3, the new variant would have an answer fairly close to 1/3. After all, knowing the birth day is a Tuesday may (and does) make a difference, but it surely cannot make much of a difference, right?

Wrong. It makes a surprisingly big difference, The correct answer to the new puzzle is 13/27, just slightly less than 1/2, and not at all close to 1/3. This is what really surprised me. To the extent that I checked my solution with the one Bellos published on his blog a few days later.

The crux of the matter is that Foshee’s variant seems at first glance to be a minor twist on the original one, but it’s actually significantly different. The property it focuses on is not gender, but the combination property [gender + day of birth]. That makes the mathematics very different, as I’ll now show.

Instead of just the two genders, B and G, of the original puzzle, there are now 14 possibilities for each child:

B-Mo, B-Tu, B-We, B-Th, B-Fr, B-Sa, B-Su

G-Mo, G-Tu, G-We, G-Th, G-Fr, G-Sa, G-Su

When I tell you that one of my children is a boy born on a Tuesday, I eliminate a number of possible combinations, leaving the following:

First child B-Tu, second child:

B-Mo, B-Tu, B-We, B-Th, B-Fr, B-Sa, B-Su,

G-Mo, G-Tu, G-We, G-Th, G-Fr, G-Sa, G-Su.

Second child B-Tu, first child:

B-Mo, B-We, B-Th, B-Fr, B-Sa, B-Su,

G-Mo, G-Tu, G-We, G-Th, G-Fr, G-Sa, G-Su.

Notice that the second grouping has one fewer members than the first, since the combination B-Tu + B-Tu already appears in the first row.

Altogether, there are 14 + 13 = 27 possibilities. Of these, how many give me two boys? Well, just count them. There are 7 in the first row, 6 in the second row, for a total of 13 in all.

So 13 of the 27 possibilities give me two boys, giving that answer of 13/27.

(As in the original problem, you have to assume all the combinations are equally likely. In the case of birth days, this is actually not the case, since more babies are born on Fridays, and fewer on weekends, due to the desire of hospital doctors to have weekends as free as possible of duties.)

What misled my intuition (and likely yours as well) was my unfamiliarity with the property [gender +day of birth]. Fortunately, the math does not lie. Provided you put your intuitions to one side and set up the problem correctly, the math will give you the right answer.

Now that your intuition has been primed, let me leave you with this problem.I tell you I have two children, and (at least) one of them is a boy born on April 1. What probability should you assign to the event that I have two boys?

If you think that is going to be too cumbersome, simply tell me whether the probability is close to 1/2 or to 1/3, or to some other simple fraction, and provide an estimate as to how close. (Once more, you should assume all birth possibilities are equally likely, ignoring in particular the well known seasonal variations in actual births.)

If you are still having doubts about all of this, take consolation in the fact that you are not alone. Representing real-world problems correctly to calculate probabilities is notoriously difficult. In my recent book The Unfinished Game, cited below, I describe how no less a mathematician than Blaise Pascal had enormous difficulty understanding an analogous argument by Pierre de Fermat.

Devlin’s Angle is updated at the beginning of each month.

MAY 2010

The problem with word problems

Last month’s column, about the probability puzzler “Boy born on a Tuesday”, generated a fair sized mailbag. An interesting feature of the emails I received is that, by and large, the pure mathematicians and puzzle specialists who wrote me did so to remark on how neat the problem was, whereas the applied mathematicians and statisticians generally cried foul.

Had I stated the problem as “Given that a man chosen at random has two children, at least one of which is a boy born on a Tuesday, what is the probability that he has two boys?” then the answer would be 13/27, as I derived. But that is not how I stated it. Rather I used a slight rewording of the problem as I came across it, which I believe was the wording with which puzzle master Gary Froshee presented is at the recent Gathering for Gardner conference. I said:

“I tell you I have two children, and (at least) one of them is a boy born on a Tuesday. What probability should you assign to the event that I have two boys?”

As my statistician correspondents observed—and I agree—with that wording, things are a lot more murky. Likewise for the simpler version I discussed, that makes no mention of the day of birth, where the “correct” answer is 1/3. At issue is the precise circumstance under which I come to impart the information I do. Why did I say what I did, and what other statements might I have made?

For example, suppose I come from a culture where it is obligatory to speak about one’s elder child before making mention of any younger siblings? Factor that additional information into the arguments I gave last time and you will find you arrive at very different answers: 1/2 in each case.

Or how about the following scenario. You know I have two children, but that’s all you know about my family. We meet in the street and I happen to have one of my children with me. I say, “Meet George, a Tuesday child.” The only rational value you can put on the probability that my other child is a boy is 1/2. (The reason being, it is, as far as you know, purely random that George is the child who accompanies me. Of course, if I came from a culture where fathers are seen in public only with sons, and in such cases all their sons, …)

Now, people who like probability puzzles (and those of us who love to hate them, or do I mean hate to love them?) know about these complications, but we learn to read them a certain way. That way is very much part of the code of pure mathematics in general, and probability questions in particular. We dress them up as real life scenarios involving one or two people, usually the puzzle poser and her or his target, to personalize them, and avoid always talking about “randomly selected individuals from a population.” But it’s just part of a genre of dressing up mathematical questions in imaginary scenarios.

It’s a genre with a long history, going back to the mathematical puzzles posed by the ancient Greeks, by the Indian and Arabic-speaking mathematicians in the first millennium, and by the European mathematicians that came after them, starting with Fibonacci in the thirteenth century, whose famous rabbit colony grew in a fashion that I doubt any biologist has ever observed. (For two further examples of unrealistic “real-world scenarios” with long histories, see the birds problems in my December 2009 column.)

Those scenarios may all use familiar words and everyday activities, but they are far from realistic. They work provided everyone knows the code and is prepared to play the game.

When such problems are used in elementary educational settings, considerable caution is required, since the recipient in such cases in all likelihood does not yet know the code. In fact, as I argue in just a moment, I think such problems should be banned from the lower grades.

But for mature students, the kind who might typically be faced with some probability theory, there is little danger. If they have gotten that far in mathematics, they have surely learned the code. And then the problem can provide an excellent launching pad to dig deep into the very issues it is designed to illustrate—namely, how do you compute probabilities (and, more fundamental, what does probability mean)? For instance, the instructor can ask the class to formulate the children’s gender problems in ways that lead to different, specific answers, and then discuss those formulations.

Case in point, one of my correspondents suggested that to get the 13/27 answer, imagine you are a witness in a court of law, and the judge, having established that you have two children, asks you, under oath, if at least one of your children is a boy born on a Tuesday. Well, maybe I’d better add the condition that the judge also says you that you must answer, giving a simple yes or no. (Though even then it is not hard to imagine how this could still be over-ridden by a further twist to the story to give a different answer.)

While the unrealistic nature of these spuriously “real-world” word problems can provide an excellent pedagogic entry point for more mature audiences, they can have potentially disastrous consequences for younger students learning mathematics for the first time.

I cringe whenever I see an elementary school textbook present a problem such as “If a quarter of a pound of ham costs $2, how much will three pounds cost?” Any child who has accompanied a parent shopping for groceries knows that things are often cheaper per pound when you buy a greater quantity. As a result, though the child may eventually learn to solve such problems the way the textbook wants, the real lesson being imparted is that mathematics is a stupid, arbitrary subject having no relevance to the real world.

Or, consider, for a moment, the following actual exchange, recorded in an elementary school classroom:

TEACHER: Alright class, here is a ratio problem for you. In order to paint a certain wall pink, a painter uses a gallon of white paint mixed with three drops of red paint. How much white and red paint would he use to paint a wall three times that size?

PUPIL: Teacher, I know! My parents run a painting company, so I learned this from them. If you paint a really big wall, you have to mix the color a little bit darker, because the sunlight falling on a large wall will make the color appear lighter. And you would have to mix up the first gallon, and then mix the other batches to a chip, because there might be a slight color difference in different job lots of paint from the factory. In any case, you wouldn’t mix up three batches of paint all at once, because the colors would start to separate before you were ready to use them. You’re usually better to trust your eye than just to go by the measurements anyway …

TEACHER: Alright! Enough! What you have to realize is that we’re not talking about painting here, we’re talking about ratio!

[Recounted in The Word Problem As Genre In Mathematics Education, by Susan Gail Gerofsky.]

Now, I suppose that, faced with such a response, a truly gifted teacher, with a lot of knowledge of mathematics, paints, painting, the physics of light, and color-cognition, who also has sufficient time available, might use the child’s fascinating response to start a highly educational investigation, but it would be hard to pull off, especially on the fly. Personally, I’d rather not introduce the problem in the first place, and thereby avoid having to crush the enthusiastic interest of the pupil who answered. (What are the chances that the child in question never again volunteered an answer to a question in the math class? Other than—perhaps—the unrealistic answer the child knows the teacher is looking for.)

Of course, many students do eventually learn to “play the game,” albeit in many cases at the cost of coming to view mathematics as having no relevance to the real world. Then we hit them with problems about how many 40-seat buses does it take to transport 500 men, and slap them down again when they answer 12 1/2. (In this case, the “right” answer is usually 13 buses. But in today’s energy conscious world, the contractor might well send down 12 40-seat buses and an additional 20-seat bus, so 12 1/2 is not at all unrealistic.)

“Oh, so we should ignore some real-world knowledge, but not all of it? Tell me, teacher, which parts should we ignore?”

The only answer, of course, is that you ignore the parts that would give an answer other than the one I want you to produce!

Which is fine if you already know the math, but hopeless as a pedagogic device to help students gain their initial understanding. I suspect the only people who survive this educational process are the ones who go on to teach math.

Talking of how we should be teaching math, I hope that by now any math teachers in my audience have seen the Youtube video of math teacher Dan Meyer’s TED talk last March. If not, please do so right now. You’ll find it below. Dan is by no means unique in his approach, though sadly he is most definitely not the norm. What singles him out is his use of online-posted home-video to broadcast his thoughts.

I hope math textbook publishers have seen Dan’s speech as well. By all appearances, they have set their sights on becoming the math ed equivalent of Fox News. (Okay, I exaggerate here.) This not in the best long term interests of the United States.

Devlin’s Angle is updated at the beginning of each month.

JUNE 2010

In math you have to remember, in other subjects you can think about it

The title of this month’s rant is a statement made by a female high school student. I’ll come back to her in due course.

The US ranks much worse than most of our economic competitors in the mathematics performance of high school students. Many attempts have been made to improve this dismal performance, but none have worked. To my mind (and I am by no means alone in thinking this), the reason is clear. Those attempts have all focused on improving basic math skills. In contrast, the emphasis should be elsewhere.

Mathematics is a way of thinking about problems and issues in the world. Get the thinking right and the skills come largely for free.

Numerous studies over the past thirty years have shown that when people of any age and any ability level are faced with mathematical challenges that arise naturally in a real-world context that has meaning for them, and where the outcome directly matters to them, they rapidly achieve a high level of competence. How high? Typically 98 percent, that’s how high. I describe some of those studies in my book The Math Gene (Basic Books, 2000). I also provide an explanation of why those same people, when presented with the very same mathematical challenges in a traditional paper-and-pencil classroom fashion, perform at a lowly 37 percent level.

The evidence is clear. It’s not that people cannot think mathematically. It’s that they have enormous trouble doing it in a de-contextualized, abstract setting.

So why the continued focus on skills? Because many people, even those in positions of power and influence, not only are totally unaware of the findings I just mentioned, they don’t even understand what mathematics is and how it works. All they see are the skills, and they think, wrongly, that is what mathematics is about. Given that for most people, their last close encounter with mathematics was a skills-based school math class, it is not hard to see how this misconception arises. But to confuse mathematics with mastery of skills is the same as thinking architecture is about bricklaying, or confusing music with mastering the musical scale.

Of course basic skills are important. But they are merely the tools for mathematical thinking. In the pre-computer era, an industrial society like the United States needed a large workforce of people with mastery of basic math skills who could carry out tasks assigned to them by others. But in today’s workplace, the coin of the realm is creative problem solving, usually in collaborative groups, making use of mathematical thinking when it is required. How well are we preparing today’s students for life in that environment? How do we compare with our competitor nations?

The answer is, not well. In an international survey conducted in 2003, students from forty countries were asked whether they agreed or disagreed with the statement: “When I study math, I try to learn the answers to the problems off by heart.” Across all students, an average of 65 percent disagreed with this statement—which is encouraging since it is a hopeless way to learn math—but 67 percent of American children agreed with it! (From Learning for Tomorrow’s World: First results from PISA 2003, OECD.)

So what are we doing wrong?

People disagree over some details, but there seems to be a wide (though not universal) consensus over three main causes:

Our mathematics curriculum (actually, it’s curricula, since each state has its own, but the complaint applies to all) contains far too many required topics, each of which can be taught only to a shallow degree—often referred to as the “mile wide, inch deep” problem.
Far too many math teachers do not have a good understanding of the subject they teach.
In the majority of classrooms, mathematics is taught in a rigid, rule-based fashion.

That caveat I made about the agreement on these three factors not being universal applies primarily to the last item in this list. Walk into any US high-school math classroom, and you will be greeted by one of two very different scenes.

In the first scene, by far the most common, you will see the students sitting in neatly organized rows, facing the teacher, who stands at the front. On the desk in front of each student you will likely see a textbook, a notebook, a pen or pencil, and perhaps a calculator. At the start of each class, the teacher will spend some time at the whiteboard, explaining some new rule or technique and working through one or two examples. Then the students will open their textbooks and proceed to work through a number of assigned examples whose solutions require the technique they have just been shown. They will for the most part work alone, and in silence. When they run into a problem, they will call on the teacher for help, not each other. When they have completed the task, the cycle begins over again. This teaching method is general known as “the traditional approach.” It’s an appropriate name, since it has been used since medieval times.

The other, less common scene appears much more chaotic. Groups of students sit around circular tables discussing how to solve a particular problem, or standing at the whiteboard arguing about the best way to proceed. The teacher moves around the room talking with the different groups in turn, making suggestions as to how to proceed, or pointing out possible errors in a particular line of reasoning the students are following. Occasionally, the teacher will call the entire group to order and ask one group to explain their solution to the rest of the class, or to give a short, mini-lecture about a particular concept or method. This is sometimes called “the progressive approach.”

The question which is the better method lies at the heart of the infamous “math wars” that have raged in California and New York (in particular). Though you can find the same two pedagogic approaches in many countries, only in the US has the issue become an issue for fierce and often angry debate.

As an outsider, coming from the UK fairly late in my career, what struck me from the start was that much of the debate comprised the setting up and knocking down of straw men. Traditionalist teachers would be accused of doing nothing but drill their students mercilessly in basic procedural skills, paying no attention to the development of mathematical concepts, while the progressives would be burned in effigy for not valuing basic skills (or seeing the need to practice them) and presenting students with a wishy-washy, watered down pap that had no real mathematical meat.

Doubtless you can find examples of each, but for the most part these caricatures exist only in the minds of the critics who make those claims, and neither is remotely correct. Rather, what you find are thousands of teachers doing the best they can, trying to balance the need for conceptual understanding with the need to practice basic skills, but unsure of what is the best way to proceed, particularly when it comes to motivating their students.

In the meantime, absent any clear evidence as to how best to proceed, the majority of teachers quite understandably default to more or less the same teaching methods that they themselves experienced. Overwhelmingly that is the traditional method, though the fact that no one has been able to make this approach work (for the majority of students) for a thousand years does make some wonder if there is a better way.

Now, at last, there is evidence, and more is being gathered. This means that raw belief and blind faith can finally start to be replaced by a reasoned choice, based on the evidence. This will surely happen, but how long it will take, after such a bitter battle, remains to be seen. Most likely the conflict will be fully put to rest only after the same has happened to some of the more prominent proponents. Meanwhile, expect to see gradual change as more teachers, parents, and politicians become aware of the rising mass of hard data.

One of the researchers who has been patiently gathering that data is Dr. Jo Boaler, and she recently published a short, readable summary of some of her findings in the form of a book: What’s Math Got To Do With It?

Though written for parents, I believe Boaler’s book should be read by everyone involved in mathematics education. You may question some of her conclusions. Indeed, some did when her work first became known in the US, around 2003, though her subsequent research has, in my view, answered some of the questions raised. But in a field like mathematics education, where conclusive hard evidence is so hard to come by, and where the majority of claims made about the efficacy of various pedagogies are based on nothing more than an extrapolation from personal experience (of the teacher, not the student), any in-depth study such as hers deserves to be seriously considered. Not least because Boaler focuses her study not on the teachers but on the students being taught. Her recent book forms the basis for the remainder of this essay. The quote I took for my title can be found on page 40.

Boaler began her career as a math teacher in her native UK, transferred to academia (London University), and was for several years a professor of mathematics education (and hence a colleague of mine) at Stanford. Then, in 2006, she returned to the UK to take up the newly established Marie Curie Chair in Mathematics Education at the University of Sussex in England, This summer, she is returning to Stanford, where we are most eager to have her back.

Over many years, Boaler conducted interviews with hundreds of students from both traditionally taught math classes and those with a more progressive approach. One of the questions she asked them what it took to be successful in math. By far the most common answer she received from students taught in a traditional fashion was to pay careful attention.

Among other answers Boaler received in schools with a traditional pedagogy, which she quotes in her book, are [p.41]:

“I’m just not interested in, first, you give me a formula, I’m supposed to memorize the answer, apply it, and that’s it.”

“You have to be willing to accept that sometimes things don’t look like – they don’t see that you should do them. Like they have a point. But you have to accept them.”

Another traditionally-taught student Boaler interviewed, called Rebecca, was conscientious, motivated, and smart, and regularly attained A+ grades in mathematics. She was able to follow the methods her teacher demonstrated in class, and could reproduce them perfectly. But she did not understand what she was doing, and as a result she regarded herself as not good at math. When Boaler asked her why she thought that, she replied, “Because I can’t remember things well and there is so much to remember.” [p.164.]

The school by the tracks

Over a four-year period, Boaler followed the progress of seven hundred students through their high school careers at three high schools. One of the three was “Railside High”. Not its real name, this school was in an urban setting, close by a railway line. She first visited the school in 1999, having heard that they seemed to be achieving remarkable results, despite the poor location and run-down appearance of the school buildings.

A number of features singled out Railside. First, the students were completely untracked, with everyone taking algebra as their first course, not just the higher attaining students. Second, instead of teaching a series of methods, such as factoring polynomials or solving inequalities, the school organized the curriculum around larger themes, such as “What is a linear function?” The students learned to make use of different kinds of representation, words, diagrams, tables symbols, objects, and graphs. They worked together in mixed ability groups, with higher attainers collaborating with lower performers, and they were expected and encouraged to explain their work to one another. [pp.58-68]

Parents whose own math education was more traditional, with the students sitting in rows, in ability-streamed classes, being shown methods by the teacher and then working silently on their own—and that is practically all parents—often find it had to believe that the Railside approach could work. They believe the loose structure will mean the kids won’t master skills well enough to pass tests, and that the presence of weaker students will drag down the better ones. Often they maintain this belief despite freely admitting that the traditional approach did not work for them, and contrary to their own experiences every day at work, where over many years they have come to know that collaborative working is highly effective, and that when someone who knows how to do something assists someone who does not, both learn and benefit from the experience.

In the nineteenth century and for much of the twentieth, most industrial workers did work silently on their own, in large open offices or on production lines, under the supervision of a manager. Schools, which have always been designed to prepare children for life as adults, were structured similarly. An important life lesson was to be able to follow rules and think inside the box. But today’s world is very different—at least for those of us living in highly developed societies. Companies long ago adopted new, more collaborative ways of working, where creative problem solving is the key to success—the ones that did not went out of business—but by and large the schools have not yet realized they need to change and start to operate in a similar fashion.

Of course, it may, as many parent seem to assume, be different in schools. After all, they will argue, what works for adults may not be successful for children. That’s a fair concern. It’s a concern that is addressed head on by Boaler’s findings. The other two schools Boaler studied along with Railside were in more affluent suburban settings, and the students started out with higher mathematics achievements than did those at the urban Railside school. Since those two schools adopted a traditional form of instruction, Boaler was able to compare student outcomes over the entire four years of high school. By the end of the first year, she found that the Railside students were achieving at the same levels as the suburban students on tests of algebra. By the end of the second year, the Railside students were outperforming their counterparts in the two suburban schools in both algebra and geometry tests. By their senior year, 41 percent of Railside students were in advanced classes of precalculus and calculus, compared to only 23 percent of students from the other two schools in more affluent neighborhoods.

What’s more, the Railside students learned to enjoy math, and saw it as useful. When Boaler and her team interviewed 105 students (mainly seniors) about their future plans, 95 percent of the students from the two suburban school said they did not intend to pursue mathematics as a subject any further, even those who had been successful. At Railside, 39 percent said they planned to take further math courses.

When Boaler would visit a class being taught in a Railside-like fashion and ask students what they were working on, they would describe the problem and how they were trying to solve it. When she asked the same questions of students being taught the traditional way, they would generally tell them what page of the book they were on. When she asked them, “But what are you actually doing?” they would answer “Oh, I’m doing number 3.” [p.98]

The Brits make the same mistake

Prior to coming to Stanford, while she was still working in her native UK, Boaler had begun a similar longitudinal study, comparing two very different schools that she called Phoenix Park (in a working class area) and Amber Hill (located in a more affluent neighborhood). The former adopted a collaborative, project-based approach, similar to Railside, the latter a more traditional pedagogy. [pp.69-83]

Boaler had chosen these two schools because, despite being in different social regions, their student intakes were demographically very similar, their entering students at age thirteen had all experienced the same educational approach, and the teachers at both schools were well qualified.

One difference between the English schools and those in California is that the UK does not follow the US practice of dividing mathematics up into separate sub-subjects, such as Algebra I, Algebra II, or Geometry; rather they just learn math (or “maths” as it’s called in Britain). But other than that, this was very much like the study she had conducted in California, and the results were strikingly similar.

At Phoenix Park, students were given considerable freedom in math classes. They were usually given choices between different projects to work on, and they were encouraged to decide the nature and direction of their work. One student explained to Boaler how they worked with these words: [p.70]

“We’re usually set a task first and we’re taught the skills needed to do the task, and then we get on with the task and we ask the teacher for help.”

Another described the process like this: [p.70]

“You’re just set the task and then you go about it … you explore the different things, and they help you in doing that … so different skills are sort of tailored to different tasks.”

In one task Boaler describes, the students were simply told that a certain object had volume 216, and asked to describe what it might look like. In another, the students were told that a farmer had thirty-six meter-long lengths of fencing and asked to find the largest area the fences could enclose.

If you think either of these is “shallow” or “not real math” then almost certainly you are living, walking proof that traditional math instruction deadens the mind to see the many possibilities each task offers, and the amount of mathematical thinking required to carry out the investigations. In her book, Boaler sketches some of the creative thinking the Phoenix Park students brought into the two tasks, and the mathematics learning that resulted. To my mind, what she describes is the early development of the creative, collaborative, problem solving skills that are essential in today’s world. As one student explained to her: [p.74]

“If you find a rule or a method, you try to adapt it to other things.”

While the Phoenix Park students were discovering that math is challenging and fun, providing an excellent outlet for their natural human curiosity, things were going very differently over at Amber Hill. There, the students worked hard, but most of them disliked mathematics. They came to believe that math was a subject that only involved memorizing rules and procedures. As one student put it: [p.75]

“In maths, there’s a certain formula to get to, say from A to B, and there’s no other way to get it. Or maybe there is, but you’ve got to remember the formula, you’ve got to remember it.”

It was at Amber Hill that a student provided Boaler with the quotation that forms the title of this month’s column.

Though the Amber Hill students spent more time-on-tasks than their counterparts at Phoenix Park, they thought math was a set of rules to be memorized. The ones that were successful did so not by understanding the mathematical ideas but by learning to follow cues. The biggest cue telling them how to solve a problem was the method the teacher had just explained on the board, or the worked example that immediately preceded it in the textbook. Another cue was to use all the information provided in the question, but nothing else.

That strategy can be made to work well until the examination at the end of the year, when those cues are not present. Predictably, even those Amber Hill students who did well during the term did poorly in those exams. And, in the national exams that all British students take at age sixteen, the Phoenix Park students easily outperformed them. Faced with a problem they did not recognize as being of a familiar type, an Amber Hill student might freeze, or struggle in vain to remember the right formula, whereas Phoenix Park students tried to make sense of it, and adapt a method they thought could be made to work.

In addition to her classroom studies at the two schools, Boaler also interviewed the students about their use of mathematics out of school. By then, many of them had weekend jobs. All forty of the Amber Hill students she interviewed declared they would never, ever make use of their school-learned methods in any situation outside school. To them, what they had been taught in the math class was a strange sort of code that can be used in only one place, the math classroom. In contrast, the Phoenix Park students were confident they would make use of the methods they had learned at school, and they gave her examples of how they had already made use of their school-learned math in their weekend jobs.

In a follow up study she conducted some years later, Boaler surveyed the then twenty-four year old graduates from Phoenix Park and Amber Hill. When they had been at school, their social class, as determined by their parents’ jobs, were the same at both schools. But eight years later, the young adults from Phoenix Park were working in more highly skilled or professional jobs than the Amber Hill adults. Demonstrating how good education can lead to upward social mobility, 65 percent of the Phoenix Park adults were in jobs more professional than their parents, compared with 23 percent of Amber Hill adults. In fact, 52 percent of Amber Hill adults were in less professional jobs than their parents, compared with only 15 percent of the Phoenix Park graduates. [pp.80-83]

Of course, you won’t get this information from reading the computer-generated scores from the standardized tests so-beloved of the US education system. Boaler does not find her data by gazing at a computer screen. She goes out and talks to the people education is all about: the students and those who were students. I ask you, which is the more important information: the score on a standardized, written test taken at the end of an educational episode, or the effect that educational episode had on the individual concerned? As a parent (if you are one), which statement would give you more pleasure?:

“Because of good teaching, my child scored 79% on her last math test,” or

“Because of good teaching, my child has a much better job and leads a far more interesting and rewarding life than me.”

Of course, teaching math in the progressive way requires teachers with more mathematical knowledge than does the traditional approach (where a teacher with a weaker background can simply follow the textbook – which incidentally is why American math textbooks are so thick). It is also much more demanding to teach that way, which makes it a job that deserves a far higher status and better pay-scale than are presently the case. And it’s a lot harder to collect the data to measure the effectiveness of the education, since it means looking at the actual products of the process: real, live people. Welcome to life in the global knowledge economy of the twenty-first century. Do you want to stay in the game, America?

If you want to know more about Boaler’s research see her book I have been quoting from and her award winning previous book Experiencing School Mathematics.

Devlin’s Angle is updated at the beginning of each month.

JULY 2010

Wanted: Innovative Mathematical Thinking

We read all the time how poorly the US mathematics education system performs compared with other nations, particularly those we compete with economically. The most cited comparison study on which this dire conclusion is reached is PISA, short for Programme for International Student Assessment, organized by the Organization for Economic Cooperation and Development (OECD).

The PISA tests are administered in schools every three years to 15-year-olds, and cover mathematics, science, and reading literacy and problem-solving skills. The main focus of the first (PISA 2000) was reading, the second (PISA 2003) mathematics, and the most recent (PISA 2006) science. (Data for the assessment that took place in 2009 will be released in December of this year.) Tests are typically administered to between 4,500 and 10,000 students in each country.

Six countries have consistently made it to the top ten: Finland, Canada, Japan, Netherlands, Australia, and New Zealand. (Singapore, which also has a very successful mathematics education system that is frequently cited, does not participate in PISA.)

In PISA 2003, out of the 30 countries in the OECD, the United States ranked 18th in mathematics, 22nd in science, and 28th in reading literacy and problem solving.

In 2006, American students ranked dead last, 25th out of 25, in math and 21st out of 30 in science.

The US also scored worse than ranked countries outside the OECD (considered to be developing nations) like Russia, Azerbaijan, Slovenia, and Estonia. Only 1 percent of American 15-year-olds could perform at the highest level, and 27 countries had a higher percentage of 15-year-olds who performed at level 6. And 28 percent of US students appear to have essentially no math skills at all.

The release of each new set of PISA results produces predictable rallying cries from politicians to “turn things around” and “put the US back at the top.” But is this realistic? And perhaps more to the point, what does it mean to be “at the top”?

At the top in what?

In terms of sheer numbers, which is the statistic of most interest to the leaders of large corporations who are faced with hiring enough mathematically-qualified employees, we cannot hope to keep up with China (population of 1.3 billion) or India (population 1.1 billion). In both countries there is enormous pressure on children to secure a good education leading to a secure future, both parental and self-motivational, and that will inevitably produce more and more highly able mathematicians, scientists, and engineers.

Will the US, with a total population of 300 million (less than a third of each of those two giants), produce individuals equal to those from China and India. Of course we will; no nation has all the world’s human talent. But in terms of the overall numbers, there is no way we will be able to keep up. So if being at the top means we produce more well qualified, able mathematical citizens than any other country, we cannot possibly succeed.

Or does being a “at the top” mean that US students will be at or near the top in international rankings such as PISA, which is the statistic that politicians seem to care most about? I seriously doubt we can achieve that. All those countries I listed that come out near the top are much smaller and cohesive than the US, and have generated systemic change in a way that our size and structure renders impossible.

To take one example, if you look at the country that came out at the very top in math on the last the PISA assessment, Finland, you find it has an educational system and societal values very different from the US:

Teachers are extremely well trained to high national certification standards, including content knowledge;
Only the best qualified applicants are admitted to education school, through a highly competitive process;
Teachers are paid a salary comparable to an engineer or a doctor;
Teaching is a highly regarded profession that many aspire to;
Teaching really is a profession, complete with peer development, regular in-service training, etc., not just a job.

By contrast, in the US:

Some states have tried to demand this only to find that there are no teachers available with many leaving the profession within five years;
Fewer and fewer students are entering the teaching profession and typically there is little or no encouragement in academic departments on campus for teachers at any level including graduate school;
Teachers’ salaries are very low compared with other professions;
Teaching is not valued and there is almost no encouragement for those entering the profession;
Professional development is required but is rarely academically oriented toward content; social issues have taken precedent in many schools.

You can, of course, lament this state of affairs all you want, but that is the playing field on which those of us with a stake in US education have to operate. So if we really want to change things (rather than just score political points and advance careers by empty rhetoric) let’s work with what we’ve got. As one of the most innovative and resourceful nations on Earth, we might just find that, in the process, we find ourselves once more in a leadership role.

The first thing we should do is admit that the existing approach simply does not work for us, and there is no way it can be made to work. Then we need to step back and take a fresh look at the situation. What exactly do we want to occur and why?

Today’s need: the innovative mathematical thinker

I’ll admit that I would like to see us adopt an education system like those in Finland or Singapore, having the features I listed above. But even if we could—and as I already indicated, I do not think it would be possible in the US—I don’t think it would be enough any more. The world has changed. In the words of author Thomas Friedman today’s world is (economically) flat. (See his book The World Is Flat: A Brief History of the Twenty-First Century.) Focusing entirely on the business and commercial worlds, traditional mathematical tasks can be outsourced even more easily than manufacturing, at digital speed with virtually no shipping cost. A designer in New York or San Francisco who wants a certain set of equations solved can simply email them to a specialist center in India and the answer will be emailed back by the next morning.

Faced with that economic reality, the only viable response for the US is to do what it has for the past century, and what we have already done with manufacturing, and stay ahead of the curve as the world’s main innovation engine. Just how long this strategy will work is hard to predict—the future usually is—but I don’t think we have a better choice.

For many years, we have grown accustomed to the fact that advancement in an industrial society required a workforce that has mathematical skills. But if you look more closely, those skills fall into two categories. The first category comprises people who can take a new problem, say in manufacturing, identify and describe key features of the problem mathematically, and use that mathematical description to analyze the problem in a precise fashion. The second category comprises people who, given a mathematical problem (i.e., a problem already formulated in mathematical terms), can find its mathematical solution.

Hitherto, our mathematics education process has focused primarily on producing people of the second variety. As it turned out, some of those people always turned out to be good at the first kind of activities as well, and as a nation we did very well. But in today’s world, and the more so tomorrow’s, with a growing supply of type 2 mathematical people in other countries—a supply that will soon outnumber our own by an order of magnitude—our only viable strategy is to focus on the first kind of ability, and hope we can hold our own in that category.

In other words, the only mathematical niche I can see for the US —and, fortunately for us, it is a crucial niche in today’s world economy—is at the innovation end. Fortunately, innovation is an area where we still lead the world, in large part because our political system allows and rewards innovation, and also because it is very much a part of the American character.

(In case that last statement comes across as being American-centric, note that it surely is simply a reflection of our history. For several centuries, and particularly the last century, some of the most innovative people from around the world have flocked to our shores to make their fortune—or in many cases simply to survive. We have a culture of, and a liking for, innovation because that was one of the consequences of large-scale immigration. We took in many of the world’s innovators, taking advantage of the fact that one country’s troublemaker can be another’s innovator!)

Traditionally, a mathematician had to acquire mastery of a range of mathematical techniques, and be able to work alone for long periods, deeply focused on a specific mathematical problem. Doubtless there will continue to be native-born Americans who are attracted to that activity, and our education system should support them. We definitely need such individuals. But our future lies elsewhere, in producing mathematical thinkers that fall into my first category above: what I propose to call the innovative mathematical thinkers.

In order to exhibit the abilities I listed in category 1 above, this new breed of individuals (well, it’s not new, I just don’t think anyone has shone a spotlight on them before) will need to have, above all else, a good conceptual (in a functional sense) understanding of mathematics, its power, its scope, when and how it can be applied, and its limitations. They will also have to have a solid mastery of basic mathematical skills, but it does not have to be stellar. A far more important requirement is that they can work well in teams, often cross-disciplinary teams, they can see things in new ways, they can quickly come up to speed on a new technique that seems to be required, and they are very good at adapting old methods to new situations.

It should go without saying that possibly the worst way to educate such individuals is to force them through a traditional mathematics curriculum, with students working alone through a linear sequence of discrete mathematical topics. To produce the twenty-first century innovative mathematical thinker, you need project-based, group learning in which teams of students are presented with realistic problems that will require mathematical and other kinds of thinking for their solution.

Of course, you still need a curriculum, in the sense of a list of topics that students need to master at some point or other. What you do not want to do is proceed through it one topic after another as is current practice in the US. A common complaint about our current, topic-by-topic, curriculum-based approach to mathematics education is that it is “a mile wide and an inch deep.” It’s not that we teach more topics overall than, say, Finland or Singapore. Rather, we try to cover too many in a single year. The countries that perform well in PISA teach far fewer topics each year, but to a far greater depth. Instead of repeating many topics year after year, those countries merely provide revision of material learned well the previous year, and focus on new topics. A well thought out project-based approach could eliminate the mile-wide, inch-deep problem as well.

The (new) role of the teacher

In the educational scenario I am describing, the teacher’s role is much more important than in the traditional system. In fact, technology has now rendered obsolete much of what teachers used to do. Except on rare occasions, today’s teacher should not be spending much time at the board explaining basic techniques. That form of instruction can now be found in videos and interactive instruction materials on the Web, much of it for free, where the student can proceed at her or his own pace, free from unwanted distractions by other students, and can stop the video at any moment, view a single frame for as long as required, and replay a segment as many times as necessary. Moreover, increasingly, such materials are being offered in a package that tracks each student’s progress and delivers new material at a rate that matches the student’s ability and past performance. (The non-profit Kahn Academy is an example of such a resource that has garnered a lot of attention of late.)

This frees the teacher from being a very expensive delivery system that ships facts from textbooks into students’ notebooks (and hopefully into the students’ minds as well), to being a full-service learning resource. Teachers can diagnose what students understand already, including their typical misunderstandings, they can offer alternative representations, counter examples, examples to help make things clearer when they have had feedback from students, they can explain misconceptions, and they can put students in situations where they have to pay attention to a new idea.

I am not saying the teacher will never stand at the board and provide instruction. A well-designed class lesson can be extremely useful. For example, some of the best designed lessons in Japan and China and Singapore can be very effective, because they draw on what students already know and anticipate plausible misconceptions that can be genuinely constructed by thinking.

But overall, modern technology changes the balance between the different activities dramatically. In the traditional approach, students were supposed to acquire new facts and learn new techniques in class, and then practice them at home. In the twenty-first century educational system, these two can be, and in my view should be, completely interchanged: home is the primary location where the student acquires the facts and learns the methods (mostly from the Web), the classroom is where, with the help of other students and the all-important teacher, the student works through exercises to gain understanding, with the teacher engaging in all the activities I listed a moment ago.

With class projects driving the entire process, it is quite likely that different students will access different material at different times, in different orders, as each team tries their own approach. In the traditional educational model, no teacher could handle that kind of information delivery load, but Web videos take care of that with ease. The “facts of math” are few. What takes time and effort is learning how to make good use of those facts—learning how to think mathematically—and that is where there is no substitute for a good (human) teacher. That’s what today’s teacher should focus her or his time on.

The leadership role that the US has been used to, and clearly wants to maintain, is to be found, I suggest, in the growing strategic importance (particularly to the US) of innovative mathematical thinking, to give a name to the kind of activity I have described above. This is where our economic future lies as a nation. And that is what our educational system needs to embrace. It is an educational philosophy that our local-control, bottom-up, free-enterprise, federated social and governmental structures, and let me add our national character, are particularly well suited to. What we should be doing is not teaching the mathematics for the industrial age, but developing in our students the kind of free-thinking, novel ways of thinking about problems, making use of mathematics when required or appropriate, that are necessary in a nation whose economic well being depends upon constantly innovating.

Devlin’s Angle is updated at the beginning of each month.

AUGUST 2010

2010: A Space Odyssey

Mathematics is finally getting its fair share of the museum world. Hot on the heels of the launch of MoMath, Glen Whitney’s Museum of Mathematics, and the Swedish Mathematics Palace I discussed in my September, 2009 column, San Francisco’s excellent Exploratorium recently launched its Geometry Playground. All of the photos in this month’s column are from the exhibit. They were taken by Amy Snyder and are copyrighted by the Exploratorium, which kindly provided them to me for display here.

The focus of the Geometry Playground is shape, with different exhibits letting the visitor explore shapes as we see things, shapes that surround us, how shapes can fit together, and shapes as they relate to motion.

Such exhibits are always fun to visit, and for those of us in mathematics education it is interesting to watch others reactions to what they see and experience, particularly young children and families. Math exhibits probably help raise awareness of mathematics concepts—in some cases by making people realize that certain things actually are mathematical concepts! But do they help students become better able to do math? The jury is largely still out on that, but the Geometry Playground is the setting for an ongoing research project being carried out by the Exploratorium to study how people approach the challenges presented by the various mathematical exhibits. Hidden away from the gaze of the museum’s visitors, a team of researchers is pouring through hours of video recordings captured by overhead cameras in the museum.

Certainly, exhibit designer Tom Rockwell, who led the design and construction of the Geometry Playground, and who took me on a tour of the exhibit recently, thinks there could be a positive classroom effect, but he will be satisfied if children, adults, and families simply have a fun few hours exploring a world of shapes. And that they are definitely doing, as I witnessed with my own eyes.

Meanwhile, that’s enough words for a column about shapes. Here are three more images from the exhibit:

**Crawl through a large scale version of the tessellation you constructed in the table-top exhibit below**

**Explore the exterior & interior** of **a large scale version of the tessellation you constructed in the table-top exhibit below**

**Can you build a pyramid with these space-filling blocks?**

The Geometry Playground remains at the Exploratorium (Palace of Fine Arts, 3601 Lyon Street, San Francisco, CA 94123) until September 6, 2010, then moves to the Science Museum of Minnesota, St. Paul, Minnesota for Fall 2010 through Winter 2011, then travels back west to the Reuben H. Fleet Science Center in San Diego, California for Summer 2011 through Spring 2012.

Devlin’s Angle is updated at the beginning of each month.

SEPTEMBER 2010

A Fibonacci photo-album

With summer coming to an end, many people share their summer snapshots with their family and friends. In that spirit, in this month’s column I’d like to share some of my summer photographs. Actually, photographs taken over several summers as I traveled to Italy to research a book about Fibonacci. That book will appear sometime next year. Meanwhile, if you are interested in vicariously treading in the footsteps of the man who brought modern arithmetic to the West, now is your chance. Along the way, you will likely discover that many of the things you believed about Fibonacci are actually false. (Especially if you learned about them on the Internet. And yes, I am aware of the irony of my making this statement in an online column!)

If you prefer a higher resolution version as an e-book in Quicktime Presentation format, you can download it from my website (it’s a 100Mb file) or play it on the Web.

Devlin’s Angle is updated at the beginning of each month.

OCTOBER 2010

Twist or bust

One of the occasional frustrations of relocating from one English speaking country to another is when a phrase well-known in one country is not widely known in another. Having grown up in the UK, the obvious title for this month’s column is the term commonly used in the card game “21” (“Blackjack” for American readers) when the dealer offers the player a chance to take another card. Every native speaker of British-English will know the phrase “twist or bust.” Now native speakers of American-English who read MAA Online know it too.

The opening image indicates why I could not resist my title. It shows a kink put into a long pipeline to prevent the pipe from fracturing when it expands in hot weather.

Which brings me to the mathematics. Imagine there is a stretch of pipe a mile long, laid in cold weather, firmly anchored at both ends. During hot weather, the pipe expands by a foot over its entire one-mile length, causing it to buckle upwards in an arch. Roughly how high will the arch be off the ground at its center (highest) point?

Before I give the answer, I should say that my point is to illustrate how bad we can be at some quantitative estimation tasks. An example that I think is better known than the pipeline puzzle is the one about wrapping a belt around the Equator.

To wrap exactly around, the length of the belt has to be the circumference of the Earth at the Equator. But what if the belt is 10ft too long? How far off the surface of the Earth will the belt be if you string it from equally tall poles all the way around? Since an excess of 10ft seems tiny when spread over the entire circumference of the Earth, our intuitions tell us the height of the belt will be too small to measure. But in fact it is about 1.5ft.

Mathematically, the issue is straightforward. An increase in the circumference of length L corresponds to an increase in diameter of length L/pi, so the 10ft excess in the belt needs a circle of diameter 10/pi more, or about 3.2ft, to accommodate the excess length, putting the belt itself about 1.6ft above the ground.

Now back to the expanding pipeline. Primed with the answer to the circumventing-belt puzzle, what is your first guess about the height of that buckle? Remember, the pipe expands by a mere 1ft over its entire one mile length.

The answer is, I think, even more surprising than in the previous puzzle. The pipe forms an arch over 50ft high. Here’s the calculation.

For simplicity, assume the pipe has a clean bend in the center, with each half remaining straight. The diagram below shows one half of the bent pipe, with the units in feet. (1 mile is 5,280ft.)

By Pythagoras’ theorem,

h² = 2640.5² – 2640² = (2640.5 + 2640)(2640.5 – 2640) = 5280.5 x 0.5 = 2640.25

so h = 51.4 (approx).

Finally, I’ll leave you with this puzzle. To the best of our knowledge, our species Homo sapiens is 200,000 years old. For a celebration of human evolution, you decide to line up a group of people to represent your entire personal lineage in the species, with you at one end holding hands with your father next to you, his father holding hands with your father, etc.

Roughly how many people will you need, and, assuming each individual occupies a width of 5ft from clasped hand to clasped hand, how long will the line be? How long would it take you to go along the line and shake hands with all your species ancestors?

Sometimes, numbers just surprise us.

Devlin’s Angle is updated at the beginning of each month.

NOVEMBER 2010

The other thing Fourier did

Quick, what first comes to mind when I mention the name Joseph Fourier?

Almost certainly, you answered “Fourier analysis” or “Fourier transform.” If not, you probably found yourself on this website by mistake. For those are what the famous French mathematician (1768-1830) is best known for to mathematicians.

Well, I suppose if your interests are the history of mathematics, you might have answered, “He is one of the first mathematicians to carry out a detailed mathematical analysis of heat flow.” But what his name probably did not evoke is the response “Greenhouse effect.” Yet he is the first person to observe a phenomenon that has become a hot (sic) topic of political discussion in the United States.

In October 1824, Fourier published a scientific paper titled “Remarques generales sur les Temperatures du globe terrestre et des espaces planetaires” in the journal Annales de Chimie et de Physique, Tome XXVII (pp.136-167), in which he presented his results from a mathematical analysis, that climate-change experts today (the ones who actually are experts) generally regard as the start of climate-change science.

Fourier stumbled across the greenhouse effect when he puzzled over this particularly tantalizing question: Every day the Sun’s rays strike the Earth’s surface and warm it up, so why doesn’t the planet keep heating up until it is as hot as the Sun itself?

His answer was that the heated surface must emit invisible infrared radiation, which carries the heat energy away into space. But when he calculated the effect mathematically, he got a temperature well below freezing, much colder than the actual Earth. The difference, he suggested, must be due to the Earth’s atmosphere. Somehow it kept part of the heat radiation in. He tried to explain this by comparing way Earth’s atmosphere holds in heat from the Sun to the way the glass of a greenhouse keeps in the heat. He actually wrote about a glass box rather than a greenhouse, but the name “greenhouse effect” for the effect he described was coined soon afterwards.

Fourier did not set out to think about climate change as such. Rather he was investigating the purely scientific question of what determines the average temperature of a planet like the Earth? This was the sort of question that physicists were just beginning to learn how to attack back in the early 19th century. To understand heat transfer, Fourier invented the powerful mathematical techniques he is best known for to mathematicians today—techniques that turned out to have many applications besides heat flow, in particular, forming the basis of modern music synthesizers and MP3 players.

In fact, Fourier’s glass box example was far too simple. It’s quite different physics that keeps heat inside a greenhouse. The main effect of the glass is to keep the air heated by contact with sun-warmed surfaces from wafting away, although the glass does also keep heat radiation from escaping.

In 1862, the Irish physicist John Tyndall gave the correct explanation for how the atmosphere retains heat. He discovered in his laboratory that certain gases, including water vapor and carbon dioxide, do not transmit heat rays. Such gases high in the air help keep our planet warm by interfering with escaping radiation. He wrote: “As a dam built across a river causes a local deepening of the stream, so our atmosphere, thrown as a barrier across the terrestrial rays, produces a local heightening of the temperature at the Earth’s surface.”

So we knew the basic scientific principle behind global warming back in 1862. But it was not until the mid-20th century that scientists would fully understand how the effect works, and with the aid of computers could calculate it with some precision. Today, we know that the actual physics is fairly complex, but a rough explanation goes like this.

Visible sunlight penetrates easily through the air and warms the Earth’s surface. When the surface emits invisible infrared heat radiation, this radiation also easily penetrates the main gases of the air. But as Tyndall found, even a trace of CO2, (a single bottle-full in his laboratory) is almost opaque to heat radiation. Thus a good part of the radiation that rises from the surface is absorbed by CO2 in the middle levels of the atmosphere. Its energy transfers into the air itself rather than escaping directly into space. Not only is the air thus warmed, but also some of the energy trapped there is radiated back to the surface, warming it further. The more CO2 there is in the atmosphere, the greater the warming.

As I noted, the actual mechanism is much more complicated than the above description. The American Institute of Physics has an excellent description on their website.

In addition to being a brilliant mathematician who became a professor at the prestigious Ecole Polytechnique in Paris, Fourier was an interesting person. He was a promoter of the French Revolution. He accompanied Napoleon on his Egyptian expedition in 1798, whereupon the emperor appointed him governor of Lower Egypt and secretary of the Institut d’Egypte. When they were cut off from France by the English fleet, he organized workshops to supply the French army with munitions. After the British victories and the capitulation of the French in 1801, Fourier returned to France, and was made prefect of Isère. It was while there that he carried out his investigations of the propagation of heat.

So now you know.

Devlin’s Angle is updated at the beginning of each month.

DECEMBER 2010

The innumeracy behind airline security

If ever I wanted to find a good example to illustrate the importance in today’s society of ensuring that citizens achieve a basic level of quantitative literacy, the recent activities at the nation’s airports provided it. Rather than spend increasing amounts of money, to say nothing of trampling on key provisions of our nation’s founding constitution (in this case the Fourth Amendment), chasing a patently unachievable target, by spending a fraction of the money on elementary mathematical education we might achieve a lot more.

I fly a lot, over 100,000 miles a year, giving me a George Clooney like (1990 Up in the Air movie), privileged 1.5 Million Miles status on United Airlines, and access to those exclusive lounges. Since a month rarely passes by without my sitting in an aircraft seat, airline safety matters to me in a very real way. My job requires that I travel a lot, so I am very aware of the risks. People die in aircraft disasters, and one day it could be me. But how likely is it?

In terms of my life being brought to a sudden, firey end in an aircraft, the cause is far more likely to be mechanical failure on the airplane or human error in the cockpit or in the airline traffic control room than it is to be a terrorist act. The airline security measures put in place shortly after 9/11 reduced the risk of dying in a terrorist attack well below the non-terrorist risks we accept every time we step on an airplane. There is absolutely no rational reason for the current level of panic-driven insanity, which as far as I can tell, having made many international trips in the past year alone, is not found in any other country, including the world’s number one potential terrorist target, Israel. The only reason I can think of for the panic in the United States is a fundamental failure to appreciate the risks.

We want our President to protect us—at least presidents keep telling us that. There are many ways a president could keep us safe. A smart move would be to allocate protective resources according to the numbers.

A nation that was truly concerned about preventing avoidable deaths would ban smoking tomorrow. It kills 440,000 people each year, according to the CDC, which works out at 50 per hour. Unlike full body scanners and intrusive “pat downs” (and yes, I’ve had one), banning smoking, while unpopular in some quarters and a threat to the livelihood of some (not a factor to take lightly), would not ride roughshod over a constitutional right.

Or how about the president getting serious about eliminating drunk driving, which kills 15,000 people in the U.S. every year, with roughly eight drunk driving fatalities involving teenagers every day.

And don’t let me start about diet, exercise, and obesity. Over 80M people in the United States have one or more forms of cardiovascular disease and over 150,000 Americans under 65 are killed by it each year; 73M have high blood pressure; 17M have coronary heart disease; over 6M suffer a stroke; and 6M have heart failure.

I’m not preaching or talking morals here. In our society we are free to make our own lifestyle decisions. It’s about the math. Spending $85M to buy 500 full body scanners at $170,000 each, and turning the simple act of boarding an airplane into a circus, to try to eliminate a risk that is orders of magnitude less than many other risks people accept in their daily lives, is a total waste of public funds, and is possible only because large numbers of people apparently don’t do—or don’t understand—the math.

It makes absolute sense to organize our lives and our society to minimize risks. But not at the expense of life itself. Life is risky. The risk of dying in your home due to a fall are far greater than of dying in a terrorist attack on an airplane. What do you do, stay in bed all the time? Actually, that isn’t a good idea. In addition to the life threatening health risks that result from not getting up and exercising, there is also a greater risk of dying by falling out of bed than from dying in an airline terrorist attack.

As a species, we find ourselves with a sophisticated brain capable of rational decision making. Since the seventeenth century we have known how to assign reliable, meaningful numbers to life’s risks so we can organize our lives appropriately. When we worry about a danger—an airline terrorist attack—that is far, far less likely than dying by drowning in our own bathtub, something has gone drastically wrong with our ability to act rationally.

Yes, the terrorist threat required action. (On a personal level, much of my mathematical research since 9/11 has been directed into ensuring we remain ahead of and catch the terrorists, so I do take the threat seriously.) We took that action in the early years after 9/11, and it has been highly effective. Have we eliminated the risk? No, that is not possible. But we have reduced it well below many of life’s other risks.

Sitting in a narrow metal tube 39,000 feet in the air is not a situation evolution prepared us for. As a consequence, at the back of my mind as I board my next flight will be all kinds of risks. But terrorism will be so far down the list as to be out of sight. The TSA’s boarding security procedures don’t give me much, if any, feeling of security. The math does. I’d stake my life on the statistics. In fact I do, several times every month.

To repeat my original point. Life in today’s society requires not only a workable level of literacy, it demands a basic level of numeracy as well. Until that level is reached, we will continue to squander scarce resources chasing unachievable and unnecessary goals, while far more important and easily attainable measures to improve lives and maintain the nation’s safety and security are ignored. Now I am preaching, so I’ll stop.

Devlin’s Angle is updated at the beginning of each month.