2006 POSTS

JANUARY 2006

Infinity and Intuition

Infinity offers many results that are at first counter-intuitive. A classic example is Hilbert’s Hotel, which has infinitely many rooms, each one labeled by a natural number printed on the door: Room 1, Room 2, Room 3, etc., all the way through the natural numbers. One night, a traveler arrives at the front desk only to be told be the clerk that the hotel is full. “But don’t worry, sir,” says the clerk, “I just took a mathematics course at my local college, and so I know how to find you a room. Just give me a minute to make some phone calls.” And a short while later, the traveler has his room for the night. What the clerk did was ask every guest to move to the room with the room number the next integer. Thus, the occupant of Room 1 moved into Room 2, the occupant of Room 2 into Room 3, etc. Everyone moved room, no one was ejected from the hotel, and Room 1 became vacant for the newly arrived guest.

This example is well known, and I expect all regular readers of MAA Online will be familiar with it. But I expect many of you will not know what happens when you step up one level of infinity. No sooner have you started to get the hang of the countable infinity (cardinality aleph-0), and you encounter the first uncountable infinity (cardinality aleph-1) and you find there are more surprises in store.

One result that surprised me when I first came across it concerns trees. Not the kind the grow in the forest, but the mathematical kind, although there are obvious similarities, reflected in the terminology mathematicians use when studying mathematical trees.

A tree is a partially ordered set (T,<) such that for every member x of T, the set {y in T : y < x} of elements below x in the tree is well ordered. This means that the tree has a preferred direction of growth (often represented as upwards in diagrams), and branching occurs only in the upward direction. It is generally assumed that a tree has a unique minimum element, called the root. (If you encounter a tree without such a root, you can simply add one, without altering the structure of the remainder of the tree.)

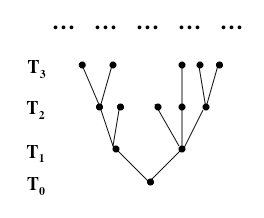
Since each element of a tree lies at the top of a unique well ordered set of predecessors, it has a well defined height in the tree – the ordinal number of the set of predecessors. For each ordinal number k, we can denote by T_k the set of all elements of the tree of height k. T_k is called the k’th level of T. T_0 consists of the root of the tree, T_1 is the set of all immediate successors of the root, etc.

Thus, the lower part of a tree might look something like this:

(It could be different. There is no restriction on how many elements there are on each level, or how many successors each member has.)

A classical result of set theory, sometimes called Konig’s Lemma, says that if T is an infinite tree, and if each level T_n, for n a natural number, is finite, then T has an infinite branch, i.e., an infinite linearly ordered subset.

It’s easy to prove this result. You define a branch {x_n : n a natural number} by recursion. To start, you take x_0 to be the root of the tree. Since the tree is infinite, but T_1 is finite, there is at least one member of T_1 that has infinitely many elements above it. Let x_1 be one such element of T_1. Since x_1 has infinitely many elements above it and yet only finitely many successors on T_2, there is at least one successor of x_1 on T_2 that has infinitely many elements above it. Let x_2 be such an element of T_2. Now define x_3 in T_3 analogously so it has infinitely many elements of the tree above it, and so on. This simple process clearly defines an infinite branch {x_n : n a natural number}.

Having seen why Konig’s Lemma holds, it’s tempting to argue by analogy that if you have an uncountable tree T (i.e., a tree whose cardinality is at least aleph-1) and if every level T_k, for k a countable ordinal, is countable, then T has an uncountable branch, i.e., a linearly ordered subset that meets level T_k for every countable ordinal k.

But it turns out that this cannot be proved. It is possible to construct an uncountable tree, all of whose levels T_k, for k a countable ordinal, are countable, for which there is no uncountable branch. Such trees are called Aronszajn trees, after the Russian mathematician who first constructed one.

Here is how to construct an Aronszajn tree. The members of the tree are strictly increasing (finite and countably transfinite), bounded sequences of rational numbers. The tree ordering is sequence extension. It is immediate that such a tree could not have an uncountable branch, since its limit (more precisely, its set-theoretic union) would be an uncountable strictly increasing sequence of rationals, contrary to the fact that the rationals form a countable set.

You build the tree by recursion on the levels. T_0 consists of the empty sequence. After T_k has been constructed, you get T_(k+1) by taking each sequence s in T_k and adding in every possible extension of s to a strictly increasing (k+1)-sequence of rationals. That is, for each s in T_k and for each rational number q greater than or equal to the supremum of s, you put into T_(k+1) the result of appending q to s. Being the countable union of countably many sets, T_(k+1) will itself be countable, as required.

In the case of regular recursion on the natural numbers, that would be all there is to the definition, but with a recursion that goes all the way up through the countable ordinals, you also have to handle limit ordinals – ordinals that are not an immediate successor of any smaller ordinal.

To facilitate the definition of the limit levels of the tree, you construct the tree so as to satisfy the following property, which I’ll call the Aronszajn property: for every pair of levels T_k and T_m, where k < m, and for every s in T_k and every rational number q that exceeds the supremum of s, there is a sequence t in T_m which extends s and whose supremum is less than q.

The definition of T_(k+1) from T_k that I just gave clearly preserves this property, since I threw in EVERY possible sequence extension of every member of T_k.

Suppose now that m is a limit ordinal and we have defined T_k for every k < m.

Given any member s of some level T_k for k < m, and any rational number q greater than the supremum of s, we define, by integer recursion, a path (s_i : i a natural number) through the portion of the tree already constructed, such that its limit (as a rational sequence) has supremum q.

You first pick some strictly increasing sequence of rationals (q_i : i a natural number) such that q_0 exceeds the supremum of s and whose limit is q.

You also pick some strictly increasing sequence (m_i : i a natural number) of ordinals less than m that has limit m and such that s lies below level m_0 in the tree.

You can then use the Aronszajn property to construct the sequence (s_i : i a natural number) so that s_i is on level m_i and the supremum of s_i is less than q_i.

Construct one such path (s_i : i a natural number) for every such pair s, q, and let T_k consist of the limit (as a sequence of rationals) of every sequence so constructed. Notice that T_k so defined is countable.

It is clear that this definition preserves the Aronszajn property, and hence the construction may be continued.

And that’s it.

Devlin’s Angle is updated at the beginning of each month.

Mathematician Keith Devlin (email: devlin@csli.stanford.edu) is the Executive Director of the Center for the Study of Language and Information at Stanford University and The Math Guy on NPR’s Weekend Edition. Devlin’s newest book, THE MATH INSTINCT: Why You’re a Mathematical Genius (along with Lobsters, Birds, Cats, and Dogs) was published recently by Thunder’s Mouth Press.

FEBRUARY 2006

Cracking the Code

April is Mathematics Awareness Month for 2006. The theme this year is Mathematics and Internet Security. (See http://mathaware.org for details.) Accordingly, this month’s column takes a look at a recent development in that field.

Chances are, you’ve never heard of Xiaoyun Wang. Unless you are a cryptographer, that is. In which case, the mere mention of her name is likely to have sent a shiver down your spine. For Wang is one of the world’s most formidable code breakers. Over the past few years, she has exposed vulnerabilities in some of the most secure digital signature systems. Fortunately, she is one of the “good guys” in the never ending struggle to keep the Internet secure, approaching the problem as an academic research project (she is currently at Tsinghua University in Beijing), publishing her methods and results, and announcing her successes at international conferences on cryptography. But if she can crack supposedly secure password systems, so can someone else, perhaps someone with more sinister motives.

Anyone who uses a computer or a bank ATM is familiar with the need to enter a password. But what is to prevent a person with criminal intent from simply monitoring the electronic signal emanating from your computer or the ATM you are using and capturing both your login name and your password and then using them to gain illegal access to your account? The answer is that the message that actually gets sent is scrambled. The most common way of scrambling identification is by means of what is called a “hash function”. Servers generally do not store your raw password, rather its scrambled version, or “hashed value”. To determine whether a login attempt is legitimate, the receiving server compares the incoming hashed login information with the hashed version of your login details stored in its database.

To make this system work in practice, the hashing function, H, has to have two fairly obvious properties:

For any input string x, it should be easy to compute H(x).
Given any hash value y, it should be computationally infeasible to find an x such that H(x) = y.

(“Computationally infeasible” means it would take the fastest computers more than (say) a human lifetime to carry out the procedure to completion.)

By requirement 2, even if a hacker gained access to the stored login information, he or she would not be able to obtain your password (though without additional controls they would of course be able to access your account on that machine, since it’s the hashed version that the receiving server uses for authorization.)

In practice, the folks who design hash functions usually demand an additional uniformity feature that facilitates efficient storage of the hashed values of identification information and makes for a faster and easier database-lookup procedure to determine identity:

All values produced by H have the same bit- length.

Because of this third condition, in theory there will be many different input strings that produce the same output; in the parlance of the hashing community, there will be “collisions”, distinct input strings x and y such that H(x) = H(y). Because access to secure sites is determined (at the site) by examining the incoming hashed login data, one possible weakness of the system is that illegal access to an account does not require that the intruder obtains the account holder’s login identity and password; it is sufficient to find some input data that generates the same hashed value, i.e. to find an input that collides with the legitimate data. In designing an algorithm for a hash function, it is therefore clearly important to make sure that this is extremely unlikely to occur. That gives a fourth requirement:

It is a practical impossibility (i.e., it is computationally infeasible) to find a string y that collides with a given string x, i.e., for which H(x) = H(y).

Typically, hash functions work by combining (in some systematic way) the bits of the input string (eg. your login details) with other bits chosen at random, and performing some complex, iterative distillation process that reduces the resulting string down to one of a fixed length (predetermined for the system).

There are dozens of different hash functions in use. The two most widely used ones are MD5 (“Message Digest algorithm 5”), developed by Ronald Rivest at MIT in 1991 as one of a series of hash algorithms he designed, and SHA-1 (“Secure Hash Algorithm 1”) developed by the National Security Agency in 1995. (Rivest is well known as one of the three inventors of the widely used RSA cryptographic system – described on the 2006 Mathematics Awareness Month website at http://mathaware.org.)

MD5 produces a hash value of 128 bits, and it would take on average 2^64 guesses to find a collision. SHA-1 generates a hash string of length 160 bits, and it would require an average of 2^80 guesses to find a collision. In theory, both methods would seem to offer a high degree of security – provided that the only feasible way to find a collision is by trial-and- error.

Enter Wang, who seems to exhibit a powerful combination of computer programming skill and a brilliant pattern recognition ability. At the Crypto 04 conference in Santa Barbara, California, Wang astonished the attendants with her announcement that she had found a way to find a collision for MD5 in just 2³⁷ inputs, a staggering reduction in problem size that made MD5 highly vulnerable.

Wang’s approach was to input to the algorithm two strings that differ by just a few bits and look closely at what happens to them, step-by- step, as the algorithm operates on them. This led her to develop a “feel” for the kinds of strings that will result in a collision, allowing her to gradually narrow down the possibilities, resulting eventually in her developing a procedure to generate a collision. Others working in the field remark that her ability to intuit which of the many possible paths to follow, coupled with her tenacity, is remarkable. Commenting to the magazine New Scientist, which covered the story in its 17 December, 2005 issue, Charanjit Jutia, a cryptographer at IBM’s Watson Research Center in Yorktown Heights, New York, described the challenge of cracking a hash function like SHA-1 as being “like a giant puzzle.” Referring to Wang, he added, “Most people get tired and give up. She did not”

In 1997, Wang used her method to successfully find collisions for SHA-0 (SHA-1’s predecessor) in 2⁵⁸ computations instead of the believed minimum of 2⁸⁰. Then, working with colleagues Dengguo Feng, Xuejia Lai, and Hongbo Yu, she developed and a variation of the same approach with MD5 that she used successfully to crack the system.

Following the announcement at Crypto 04, Wang and Yu teamed up with Yiqun Lisa Yin, now an independent security consultant based in Greenwich, Connecticut, and started work on the crown jewel of current hash functions, SHA-1. This proved a much harder nut to crack, but to the general dismay (and admiration) of the computer security community, at the annual RSA security conference in San Francisco in February last year, they were able to announce that they had developed an algorithm that could generate two SHA-1 colliding files in just 2⁶⁹ steps.

Unlike MD5, Wang and her colleagues have not (yet) cracked SHA-1, they have just produced a method that could crack it in far fewer steps than was previously believed possible. That number 2⁶⁹is still sufficiently high to provide some degree of confidence in the system’s security – for now. So too is the even lower number of 2⁶³ steps that Wang and other collaborators managed to achieve in the months following the February 2005 announcement. But many in the cryptographic community now believe that the writing is on the wall, and that, as a result of Wang’s work, advances in computing speed and power will rapidly render useless all the hashing algorithms currently in use. Not today – the experts assure us that our ATM transactions are secure for now. But soon. Commenting on the development to New Scientist, Burt Kaliski, the head of RSA Laboratories in Bedford, Massachusetts, declared “This is a crisis for the research community.” Mark Zimmerman, a cryptographer with ICSA Labs in Mechanicsburg, Pennsylvania, put it rather more colorfully. “It’s not Armageddon,” he said, “but it’s a good kick in the pants.”

I will just add that, what I think may be of particular interest to readers of MAA Online is that the entire story shows that, even in the Moore’s Law driven world of massively large computations, the remarkable pattern-recognition capacity and “numerical intuitions” of the human brain, can still play a major—indeed devastating—role. Especially when combined with another valuable human trait: tenacity.

NOTE: For further details on this story, see the article “Busted! A Crisis in Cryptography,” by Celeste Biever, in the 17 December, 2005 issue of New Scientist, available online to magazine subscribers at http://www.newscientist.com/home.ns. See also the highly informative account by the leading security consultant Bruce Schneier online at http://www.schneier.com/blog/archives/2005/02/ sha1_broken.html.

Devlin’s Angle is updated at the beginning of each month.

MARCH 2006

How do we learn math?

As a general rule, I try to stay away from the front lines of the math wars, having always felt that the real wisdom about math ed is to be found in the no man’s land between the two opposing camps. But President Bush’s call for more and better math teachers in his recent State of the Union address led my local newspaper, the San Jose Mercury News, to ask me to pen an Op Ed on the subject. This I duly did, and my piece appeared on Sunday February 19. Attacks (fairly mild, I have to say) predictably followed from both sides, leading me to believe that my remarks probably came out more or less as I intended them to, as a call for reason. In any event, I survived my brief skirmish into dangerous waters sufficiently to be tempted to stick my foot into the pond once again. So here goes.

Much of my rationale for believing that the way forward in math ed is to be found in the DMZ of the war comes from my recognition that on both sides you find significant numbers of smart, well-educated, well-meaning people, who genuinely care about mathematics education. Unless you are of the simplistic George W. mindset, that the world divides cleanly into righteous individuals on the one side and “evil doers” on the other, it follows, surely, that both sides have something valuable to say. (“Evil doers” always stuck me as a strange phrase to hear uttered in public by a grown-up, by the way. It sounds more like the box-copy description of a band of orcs in a fantasy video game.) The challenge, then, is to reconcile the two views.

In brief, the gist of my Mercury News opinion piece was this. While it sounds reasonable to suggest that understanding mathematical concepts should precede (or go along hand-in-hand with) the learning of procedural skills (such as adding fractions or solving equations), this may be (in practical terms, given the time available) impossible. The human brain evolved into its present state long before mathematics came onto the scene, and did so primarily to negotiate and survive in the physical world. As a consequence, our brains do not find it easy to understand mathematical concepts, which are completely abstract. (This is part of the theme I pursued in my book The Math Gene, published in 2000.)

However, although we are not “natural born mathematicians,” we do have three remarkable abilities that, taken together, provide the key to learning math. One is our language ability—our capacity to use symbols to represent things and to manipulate those symbols independently of what they represent. The second is our ability to ascribe meaning to our experiences—to make sense of the world, if you like. And the third is our capacity to learn new skills.

When we learn a new skill, initially we simply follow the rules in a mechanical fashion. Then, with practice, we gradually become better, and as our performance improves, our understanding grows. Think, for example, of the progression involved in learning to play chess, to play tennis, to ski, to drive a car, to play a musical instrument, to play a video game, etc. We start by following rules in a fairly mechanical fashion. Then, after a while, we are able to follow the rules proficiently. Then, some time later, we are able to apply the rules automatically and fluently. And eventually we achieve mastery and understanding. The same progression works for mathematics, only in this case, as mathematics is constructed and carried out using our language capacity, the initial rule-following stuff is primarily cognitive-linguistic.

Of course, there is plenty of evidence to show that mastery of skills without understanding is shallow, brittle, and subject to rapid decay. Understanding mathematical concepts is crucially important to mastering math. The question is: What does it take to achieve the necessary conceptual understanding, and when can it be acquired? Certainly my own experience is that conceptual understanding in mathematics comes only after a considerable amount of procedural practice (much of which therefore is of necessity carried out without understanding). How many of us professional mathematicians aced our high school or college calculus exams but only understood what a derivative is after we had our Ph.D.s and found ourselves teaching the stuff?

In fact, I can’t imagine how one could possibly understand what calculus is and how and why it works without first using its rules and methods to solve a lot of problems. Likewise for most other areas of mathematics. In fact, the only parts of mathematics that I find sufficiently close to the physical and social world our brains developed to handle that there are innate meanings we could tap into, are positive integer addition and subtraction for fairly small numbers, and perhaps also some fairly simple cases of division for small positive integers.

Interestingly, those were the only examples cited by the readers of my Mercury News article who argued against my suggestion that understanding comes only after a lot of procedural practice. Now it may be that in those particular areas, understanding can precede, or accompany the acquisition of, procedural mastery. Personally I doubt it, but I have yet to see convincing evidence either way. But, leaving those special (albeit important) cases aside, what about the rest of mathematics? Here I see no uncertainty. Understanding can come only after procedural mastery.

For example, physics and engineering faculty at universities continually stress that what they want their incoming students to have above all is procedural mastery of mathematics as a language—it is, after all, the language of science, as Galileo observed—and the ability to use various mathematical tools and methods to solve problems that arise in physics and engineering. Since even first-year physics and engineering involve use of tools such as partial differential equations, there is no hope that incoming students can have conceptual understanding of those tools and methods. But by a remarkable feature of the human brain, we can achieve procedural mastery without understanding. All it takes is practice. One of the great achievements of mathematics over the past few centuries has been the reduction of conceptually difficult issues to collections of rule-based symbolic procedures (such as calculus).

Thus, one of the things that high school mathematics education should definitely produce is the ability to learn and be able to apply rule-based symbolic processes without understanding them. Without that ability, progress into the sciences and engineering is at the very least severely hampered, and for many people may be cut off. (This, by the way, is the only rationale I can think of for teaching calculus in high school. Calculus is a supreme example of a set of rule-based procedures that can be mastered and applied without any hope of anything but the most superficial understanding until relatively late in the game. Basic probability theory and statistics are clearly far more relevant to everyday life in terms of content.)

Is mastery of rule-based symbolic procedures the only goal of school mathematics education? Of course not. The reason I am not focusing on conceptual issues is that much has been written on that issue—of particular note the National Research Council’s excellent volume Adding it Up: Helping Children Learn Mathematics, published by the National Academy Press in 2001 (a book I have read from cover to cover on three separate occasions). My intention here is to shine as bright a light as possible on a mathematical skill that I think has, in recent years, been overlooked—and on occasion actively derided—by some in the math ed community. Life in today’s society requires that we acquire many skills without associated understanding—driving a car, operating a computer, using a VCR, etc. Becoming a better driver, computer user, etc. often requires understanding the technology (and perhaps also the science behind it). But from society’s perspective (and in many cases the perspective of the individual), the most important thing is the initial mastery of use. If something has been so well designed or developed that proficient use can be acquired without conceptual understanding, then the rapid acquisition of that skillful use is often the most efficient—and sometimes the only—way for an individual to move ahead. I think this is definitely the case with mathematics. I believe we owe it to our students to prepare them well for life in the highly technological world they will live in. In the case of mathematics, that means that one ability we should equip them with (not the only one by any means—Adding It Up lists several others, for instance) is being able to learn and apply rule-based symbolic processes without understanding them. That does not mean we should not provide explanations. Indeed, as a matter of intellectual courtesy, I think we should. But we need to acknowledge, both to ourselves and our students, that understanding can come only later, as an emergent consequence of use. (No shame in that. It took 300 years from Newton’s invention of calculus to a properly worked out conceptual basis for its rules and methods.)

Devlin’s Angle is updated at the beginning of each month.

APRIL 2006

How a wave led to a prize

This year’s Mathematics Awareness Month—this month in fact—sees the MAM celebrate its 20th birthday, the annual festival having been first launched in 1986. With this year’s theme being Mathematics and Internet Security, it is perhaps fitting that it is also the 30th anniversary of the introduction by Whitfield Diffie and Martin Hellman of the idea of Public Key Cryptography. To find out more about MAM and what Diffie and Hellman did, click over to the Mathematics Awareness Month Website at www.mathaware.org, where you will find various articles describing the different ways that mathematics plays important roles in Internet Security.

The remainder of this month’s column has nothing to do with either Mathematics Awareness Month or Internet security—at least as far as I know. But having found myself organizing the MAM national campaign this year, I couldn’t resist giving it one final plug.

What I really want to talk about is the recent awarding of the Abel Prize to Swedish mathematician Lennart Carleson.

The idea for the prize, awarded annually by the Norwegian Academy of Science and Letters for work in mathematics, goes back to the start of the twentieth century. Observing that when Swedish scientist, industrialist, and philanthropist Alfred Nobel established the Nobel Prizes in 1895, he did not stipulate a prize for mathematics, the Norwegian government at the time decided to fill what they saw as an unfortunate gap and create an equivalent prize for mathematicians. They further decided that the prize should be named after the man who was arguably Norway’s most famous mathematician of all time, Niels Henrik Abel, who had lived in the early part of the 19th century. Unfortunately, the breakup of the Swedish-Norwegian union in 1905 prevented the completion of the prize creation process, and it was not until 2003 that the Norwegian government finally made good on the century-old intention of their predecessors.

With this year’s award, the prize goes to a Scandinavian for the first time. Announcing the 2006 award on 23 March, Norwegian Academy President Ole Didrik Laerum cited Lennart “for his profound and seminal contribution to harmonic analysis and the theory of smooth dynamical systems.” Lennart will receive his prize from Queen Sonja of Norway at a ceremony in Oslo on 23 May.

The result for which Lennart is most widely known is his completion of the work on wave analysis begun by Jean Baptiste Joseph Fourier (1768-1830)—Fourier analysis, the basis of today’s music synthesizers, iPod music players, and so forth. Fourier showed how to take the graph of a wave, such as a sound wave or heat radiation, and decompose it into an infinite sum of sine waves. Fourier’s approach worked for all of the naturally occurring waves that people looked at, but would it work for all waves? Or were there some strange pathological waves that could not be expressed as an infinite sum of sine waves? That question remained open for many years until Carleson answered it in 1966, showing that the Fourier decomposition process does indeed work for all waves.

For most mathematicians, one result of that magnitude in a lifetime would be more than enough, but Carleson scored big a second time in 1991, when, together with his colleague Michael Benedicks, he gave a rigorous proof of an “order out of chaos” result that had been suggested by computer work but had long resisted definite proof—namely the existence of a so-called strange attractor for a certain widely studied dynamical system known as the Henon system.

For more details about Carleson’s work and on the Abel Prize, see the Abel Prize website at www.abelprisen.no/en/

Oh, and one final thing. Please do not write to tell me that you once heard that the reason there is no Nobel Prize in Mathematics is that Nobel feared that the great Swedish mathematician Gosta Mittag-Leffler might win such a prize, and Nobel hated him for having an affair with his wife. This story is not true. It could not possibly be, since Nobel never married.

Devlin’s Angle is updated at the beginning of each month.

MAY 2006

The Mathematics of Aircraft Boarding

What is the most efficient way to board a passenger aircraft? This question occurred to me as I shuffled down the aisle of a Boeing 777 at San Francisco Airport on my way to give a lecture in Italy at the start of this month. I felt sure that some mathematicians must have studied this problem, and sure enough, a quick Web search when I got to London revealed the recent paper Analysis of Airplane Boarding Times, by Eiten Bachmat, Daniel Berend, Luba Sapir, Steven Skiena, and Natan Stolyarov. Besides presenting the results of their own research, these co-authors describe the conclusions of several earlier studies.

The standard procedure adopted by all the airlines I regularly fly with is to group passengers and board the groups one at a time, starting with First Class, then Business, then finally the Coach Class in groups starting from the back of the plane. The inefficiencies in this procedure are obvious to anyone who flies with any regularity. For airplanes where the boarding door is at the front, the bulk of the passengers have to wait until the (often less agile) first and business class passengers have stashed away their bags and taken their seats, while for airplanes that board further down the plane, with first class to the left (front) of the boarding door and economy to the right (rear), the opportunity is lost of having the front and rear portions of the plane fill up at the same time.

It seems pretty clear that, from a purely mathematical point of view, the most efficient boarding process for an airplane that boards from the front would be to linearly order all passengers, starting with those at the back of the plane, ordered from outside (window seat) inwards (aisle seat last), and then working forward. But managing such a process would be a nightmare, and the confusions inevitably caused by trying to line the passengers up in this fashion would surely make matters even worse than they already are, to say nothing of making passengers feel even more like cattle being transported to market than is already the case. (British Airways staff used to make a fetish of treating passengers badly in that regard; things may have improved, but after a series of bad experiences with bossy BA staff back in the 80s, for the past twenty-five years I have avoided flying BA as much as possible, and taken most of my flying business to United. Others may have different experiences.)

Moreover, with First and Business Class passengers expecting (with considerable justification) preferential treatment in return for paying several times more for their ticket, and with high-mileage gold card flyers like myself also expecting a “special deal” in exchange for our many hours spent in the air, it would be business suicide for any airline to ignore the many human aspects of flying.

My suspicion as I stood patiently in line on United 930 at the gate in San Francisco, watching as those ahead of me sorted themselves (and their baggage) out, was that a purely random boarding process was probably more efficient than the current systems, since boarding by class or by airplane section leads to localized congestion. And indeed, that is one of the conclusions reached by Bachmat at al in their recent paper. It also seems believable, at least to my mathematical mind, that allowing as much randomness as possible into a system designed to give some preference to First Class, gold card flyers, families-flying-with-small-children, etc. would also speed up the boarding process. But the mathematics does become pretty complicated, once you realize the different variables that are involved. Besides the position of the door (or doors), other factors that affect the boarding process are the number and width of the aisles, the number of seats per row, and the separation between the rows. Each of these parameters is built in to the mathematical model that Bachmat and his colleagues developed.

In order to capture the various complexities of the problem, the researchers use some highly sophisticated mathematics to construct a computer model that can simulate different boarding strategies for different aircraft layouts. How sophisticated? How about Lorenzian geometry, developed to handle relativity theory?

Why that geometry? you may ask. Well, the boarding process is a space-time universe, and the total time it takes to board the aircraft is the length of the longest path in that universe. Obvious once it is pointed out, isn’t it? A great example of how mathematics developed for one purpose can find a good use in an entirely different domain.

The conclusion? Summarizing runs of their computer model for various aircraft configuration, Bachmat et al observe that if the airlines were able to adopt a fairly rigid system, then outside-in boarding is much better than back-to-front, but that, overall, given passenger resistance to being strongly regimented, and recognizing the airlines’ desire to continue their different passenger-pleasing preference policies, the most efficient method seems to be—are you listening United?—a policy that combines the various customer-satisfaction policies with a hefty dose of outside-in boarding and just a touch of back-to-front; otherwise as much randomness as possible.

Devlin’s Angle is updated at the beginning of each month.

JUNE 2006

Letter to a calculus student

Dear Calculus Student,

Let me begin with a quotation from the great philosopher Bertrand Russell. He wrote, in Mysticism and Logic (1918): “Mathematics, rightly viewed, possesses not only truth, but supreme beauty-a beauty cold and austere, like that of sculpture, without appeal to any part of our weaker nature, without the gorgeous trappings of painting or music, yet sublimely pure, and capable of a stern perfection such as only the greatest art can show.”

Beauty is one of the last things you are likely to associate with the calculus. Power, yes. Utility, that too. Hopefully also ingenuity on the part of Netwon and Leibniz who invented the stuff. But not beauty. Most likely, you see the subject as a collection of techniques for solving problems to do with continuous change or the computation of areas and volumes. Those techniques are so different from anything you have previously encountered in mathematics, that it will take you every bit of effort and concentration simply to learn and follow the rules. Understanding those rules and knowing why they hold can come only later, if at all. Appreciation of the inner beauty of the subject comes later still. Again, if at all.

I fear, then, that at this stage in your career there is little chance that you will be able to truly see the beauty in the subject. Beauty—true, deep beauty, not superficial gloss—comes only with experience and familiarity. To see and appreciate true beauty in music we have to listen to a lot of music—even better we learn to play an instrument. To see the deep underlying beauty in art we must first look at a great many paintings, and ideally try our own hands at putting paint onto canvas. It is only by consuming a great deal of wine—over many years I should stress—that we acquire the taste to discern a great wine. And it is only after we have watched many hours of football or baseball, or any other sport, that we can truly appreciate the great artistry of its master practitioners. Reading descriptions about the beauty in the activities or creations of experts can never do more than hint at what the writer is trying to convey.

My hope then is not that you will read my words and say, “Yes, I get it. Boy this guy Devlin is right. Calculus is beautiful. Awesome!” What I do hope is that I can at least convince you that I (and my fellow mathematicians) can see the great beauty in our subject (including calculus). And maybe one day, many years from now, if you continue to study and use mathematics, you will remember reading these words, and at that stage you will nod your head knowingly and think, “Yes, now I can see what he was getting at. Now I too can see the beauty.”

The first step toward seeing the beauty in calculus—or in any other part of mathematics—is to go beyond the techniques and the symbolic manipulations and see the subject for what it is. Like a Shakespearean sonnet that captures the very essence of love, or a painting that brings out the beauty of the human form that is far more than just skin deep, the true beauty of calculus can only be fully appreciated by digging deep enough.

The beauty of calculus is primarily one of ideas. And there is no more beautiful idea in calculus than the formula for the definition of the derivative:

(*) f'(x) = lim_{h -> 0}[f(x+h) – f(x)]/h

For this to make sense, it is important that h is not equal to zero. For if you allow h to be zero, then the quotient in the above formula becomes

[f(x+0) – f(x)]/0 = [f(x) – f(x)]/0 = 0/0

and 0/0 is undefined. Yet, if you take any nonzero value of h, no matter how small, the quotient

[f(x+h) – f(x)]/h

will not (in general) be the derivative.

So what exactly is h? The answer is, it’s not a number, nor is it a symbol used to denote some unknown number. It’s a variable.

What’s that you say? “Isn’t a variable just a symbol used to denote an unknown number?” The answer is “No.” Sir Isaac Newton and Gottfried Leibniz, the two inventors of calculus, knew the difference, but as great a mind as the famous 18th Century philosopher and theologian (Bishop) George Berkeley seemed not to. In his tract The analyst: or a discourse addressed to an infidel mathematician, Berkeley argued that, although calculus led to true results, its foundations were insecure. He wrote of derivatives (which Newton called fluxions):

“And what are these fluxions? The velocities of evanescent increments. And what are these same evanescent increments? They are neither finite quantities, nor quantities infinitely small, nor yet nothing. May we not call them ghosts of departed quantities?”

The “evanescent increments” he was referring to are those h’s in formula (*). Berkeley’s problem—and he was by no means alone—was that he failed to see the subtlety in the formula. Like any great work of art, this formula simultaneously provides you with different ways of looking at the same thing. If you look at it just one way, you will miss its true meaning. It also asks you, nay like all great works of art it challenges you, to use your imagination—to go beyond the experience of your senses and step into an idealized world created by the human mind.

The expression to the right of the equal sign in (*) represents the result of a process. Not an actual process that you can carry out step-by-step, but an idealized, abstract process, one that exists only in the mind. It’s the process of computing the ratio

[f(x+h) – f(x)]/h

for increasingly smaller nonzero values of h and then identifying the unique number that those quotient values approach, in the sense that the difference between those quotients and that number can be made as small as you please by taking values of h sufficiently small. (Part of the mathematical theory of the derivative is to decide when there is such a number, and to show that if it exists it is unique.) The reason you can’t actually carry out this procedure is that it is infinite: it asks you to imagine taking smaller and smaller values of h ad infinitum.

The subtlety that appears to have eluded Bishop Berkeley is that, although we initially think of h as denoting smaller and smaller numbers, the “lim” term in formula (*) asks us to take a leap (and it’s a massive one) to imagine not just calculating quotients infinitely many times, but regarding that entire process as a single entity. It’s actually a breathtaking leap.

In Auguries of Innocence, the poet William Blake wrote:

To see a World in a Grain of Sand
And a Heaven in a Wild Flower
Hold Infinity in the palm of your hand
And Eternity in an hour

That’s what formula (*) asks you to do: to hold infinity in the palm of your hand. To see an infinite (and hence unending) process as a single, completed thing. Did any work of art, any other piece of human creativity, ever demand more of the observer? And to such enormous consequence for Humankind? If ever any painting, novel, poem, or statue can be thought of as having a beauty that goes beneath the surface, then the definition of the derivative may justly claim to have more beauty by far.

Devlin’s Angle is updated at the beginning of each month.

JULY-AUGUST 2006

Ten Years On

Devlin’s Angle is ten years old this year. The column began when MAA Online launched on January 1, 1996. You get some sense of the degree to which communications media have changed over those ten years when you re-read my words from that very first column:

Welcome to the new MAA on-line information service, and to my own particular corner—though the “corner” metaphor does not transfer well from the paper page to the scrolling screen. In fact, the vocabulary we use is just one of a number of things that have to change as we move to ever greater use of electronic media in our daily business.

If you are reading these words, then you have already taken the plunge and made at least the first tentative steps into the strange new world of the World Wide Web. And it really is a different world, with different rules, different advantages, and different dangers.

How quickly we all adapted to that new world.

The principal “dangers” I was referring to were computer viruses spread by email. Back then, ten years ago, spam, Internet pornography, and children’s Websites that provide a stalking ground for pedophiles were still way in the future.

Several of my early columns were based on, or related to, my then-new book Goodbye Descartes, which described Humankind’s quest to develop a mathematics of human thought, starting from the ancient Greeks’ attempts to develop a mathematical logic, moving on through the medieval scholars, on to Boole, and then into the computer era, in particular the push to develop artificial intelligence.

I’ve always been a fan of AI, indeed on one occasion I nominated (successfully) AI founder John McCarthy for an honorary degree. Yet I have always felt that AI’s importance was as much in what we learned about human thought from the enterprise’s failures (to produce intelligent behavior) as from the technologies that AI led to, and Goodbye Descartesargued that there are definite limits to the degree to which human thought can be captured or modeled by mathematics. (Hence the book’s title.)

The other two themes that the column addressed in its first year were (i) the (changing) role of mathematics in society and the ever greater need for mathematicians to work with people from other disciplines, and (ii) the changing nature of mathematics itself, as the community reflected on the evolving concept of mathematical proof.

There was also one column (September 1996) addressed to students, in particular incoming university students. Education has, of course, been changed by new information and communication technologies at least as much as the rest of our lives. And I’m not just thinking about the use of technology in the educational process. As a result of growing up in a world of computers, mobile phones, instant messaging, graphing calculators, and videogames, today’s students are simply different from their predecessors when it comes to learning.

To take one example, in their book Got Game, How the Gamer Generation is Reshaping Business Forever, John Beck & Michael Wade list some of the principal cognitive features that you find among young people who have grown up playing computer games:

Failure doesn’t hurt
Risk is part of the game
Feedback needs to be immediate
Used to being the “star”
Trial and error is almost always the best plan
There’s always an answer
I can figure it out
Competition is fun and familiar
Bosses and rules are less important
Used to group action and conflict

Got Game is aimed at the business world. It focuses on the managerial skills many games develop. Those skills include problem solving, resource management, decision making under uncertainty, decision making under pressure, multitasking, and (particularly the multi-player online games) interpersonal skills and organizational ability. (The US Army was one of the first large organizations to spot these positive learning outcomes from videogames and has invested many millions of dollars into their development and use. Many large corporations also use them to train their managers.)

Clearly, however, Beck and Wade’s list is highly relevant to those of us in the business of teaching mathematics, for the very obvious reason that it describes the approach to learning of many of our students. How many? Close to 100 percent according to recent surveys, such as a recent study of 524 fifth- through eighth-graders in Michigan and California, which found that 93 percent of girls and 97 percent of boys play video games on a regular basis.

Most leading mathematics educational thinkers would argue that all but one of the features that Beck and Wade list are precisely the characteristics of a good learner and a desirable learning environment. The one exception would surely be number 5, but that is more a feature of the simplistic way the authors state the principle. Successful game play almost always requires guided trial and error, where the player learns from previous experience in the game what attempts to avoid and what is best to try first. (It is possible to argue that 6 is also not in tune with the real world, including real world applications of mathematics, but confinement to problems that have answers does seem to be a universal feature of our entire educational system, and maybe there is a good educational reason for that.)

Item number 9 may worry some educators, but if all those recent studies of gamers are correct, it’s now an unavoidable fact of educational life. Those nine characteristics describe features of the students we are actually faced with teaching.

It seems to me that those of us in the math ed biz need to try as best we can to see the world through the same eyes as the gamer students in our classrooms, and adjust our instructional methods accordingly. That may involve providing learning experiences that are suited to their instinctive, experimental approach. Or, if we feel that learning mathematics is best done in a rule-based way, it may require that we accept that part of our job is to help them learn how to survive and prosper in a more rule dominated environment. In any event, I don’t think that we are anything like yet done with the changes in our lives resulting from new developments in information and communications technologies. The next ten years will, I believe, be every bit as interesting as the last.

Devlin’s Angle is updated at the beginning of each month.

SEPTEMBER 2006

Statisticians not wanted

On August 16, 2006, the California Supreme Court made it official: in certain legal cases that hinge on statistical calculations, it is not the business of professional statisticians to decide how to evaluate the statistical data and to judge what method is most suited to analyze that data. From now on, in California at least, the courts will decide what statistical analysis is appropriate and what is not.

It gets worse—especially if you are a professional statistician. By upholding a ruling by a lower state court, the California Supreme Court also affirmed that, in their view, the proper job for statisticians is simply to plug numbers into a formula and turn the crank to produce an answer. Not any formula will do, mind; if you want your calculation to play a rule in a California legal proceeding, it will have to be the formula chosen by the court. As a professional statistician, you may believe that it is precisely your job to make that call, and that no other profession has the knowledge, expertise, experience, and skill to make such a decision in your stead. But the California Supreme Court says otherwise. They say the decision is theirs to make. You don’t believe me? Read on.

The issue is one of suspect identification and conviction based on DNA profiling. Since both the reliability of a “DNA (profile) match” as a means to identify a suspect in a criminal investigation and its efficacy as evidence in court depend upon the likelihood of two different individuals sharing the same profile, use of the technique is crucially dependent on calculation of that likelihood. That’s where statistics comes into the picture.

It turns out, however, to be not at all an obvious matter how to compute the appropriate statistic—or more precisely, to decide what exactly is the appropriate statistic. To my mind, though not the mind of the California Supreme Court it appears, that is where statisticians should come into the picture.

To take the story any further, I need to provide a brief summary of the DNA profiling technique.

DNA profiling

The DNA molecule comprises two long strands, twisted around each other in the now familiar double-helix structure, joined together in a rope-ladder-fashion by chemical building blocks called bases. (The two strands constitute the “ropes” of the “ladder”, the bonds between the bases its “rungs”.) There are four different bases, adenine (A), thymine (T), guanine (G), and cytosine (C). The human genome is made of a sequence of roughly three billion of these base-pairs. Proceeding along the DNA molecule, the sequence of letters denoting the order of the bases (a portion might be … AATGGGCATTTTGAC …) provides a “readout” of the genetic code of the person (or other living entity). It is this “readout” that provides the basis for DNA profiling.

Using today’s techniques, it would be totally impractical to do a DNA comparison by determining all three billion letters. What is done instead is to examine a very small handful of sites of variation.

DNA is arranged into large structural bodies called chromosomes. Humans have 23 pairs of chromosomes which together make up the human genome. One chromosome in each pair is inherited from the mother and the other from the father. This means that an individual will have two complete sets of genetic material. A “gene” is really a location (locus) on a chromosome. Some genes may have different versions, which are referred to as “alleles.” A pair of chromosomes have the same loci all the way along their length, but may have different alleles at some of the loci. Alleles are characterized by their slightly different base sequences and are distinguished by their different phenotypic effects. Some of the genes studied in forensic DNA tests have as many as 35 different alleles in the population.

Most people share very similar gene sequences, but some regions of DNA sequence vary from person to person with high frequency. Comparing variation in these regions allows scientists to answer the question of whether two different DNA samples come from the same person.

The profiling technique used by the FBI and other law enforcement authorities depends on the fact that the variability is manifested by differences in the length, measured by the number of bases or the number of times a given sequence repeats, between pre-specified locations. This procedure yields two measurements for each sample for each locus, one for the father’s side and one for the mother’s side. The length of DNA fragments can be measured precisely. In comparing two samples at a given locus, if the pair of measurements from one sample is the same as the pair of measurements from the other, the profiles are said to match at that locus; otherwise, they are said not to match at that locus. If the two profiles match at each of the loci examined, the profiles are said to match. If the profiles fail to match at one or more loci, then the profiles do not match, and it is virtually certain that the samples do not come from the same person.

A match does not mean that the two samples must absolutely have come from the same source; all that can be said is that, so far as the test was able to determine, the two profiles were identical, but it is possible for more than one person to have the same profile across several loci. At any given locus, the percentage of people having DNA fragments of a given length, in terms of base pairs, is small but not zero. DNA tests gain their power from the conjunction of matches at each of several loci; it is extremely rare for two samples taken from unrelated individuals to show such congruence over many loci.

The FBI’s forensic DNA identification system (called CODIS) examines thirteen such regions in the genome. Sequences in these special regions involve multiple repetitions of short combinations of letters, such as GATA. Easily detectable differences between people lie in the number of repeats that occur in both copies of their DNA in these regions. For example, at one of these regions a person might have inherited four repeats (GATAGATAGATAGATA) from their father and six repeats (GATAGATAGATAGATAGATAGATA) from their mother at the same location in the genome. Another person might inherit eight repeats (GATAGATAGATAGATAGATAGATAGATAGATA) from their father and five repeats (GATAGATAGATAGATAGATA) from their mother.

How reliable is DNA profile matching

When two randomly chosen DNA samples match completely in a large number of regions, such as the 13 used in the FBI’s system, the probability that they could have come from two unrelated people is very small. This fact makes DNA identification extremely reliable (when performed correctly). The degree of reliability is generally measured by using the product rule of probability theory to determine the likelihood of finding a particular profile among a random selection of the population.

For example, consider a profile based on just three sites. The probability that someone would match a random DNA sample at any one site is roughly one in ten (1/10). So the probability that someone would match a random sample at three sites would be about one in a thousand:

1/10 x 1/10 x 1/10 = 1/1,000.

Applying the same probability calculation to all 13 sites used in the FBI’s CODIS system would mean that the chances of matching a given DNA sample at random in the population are about one in ten trillion:

(1/10)¹³= 1/10,000,000,000,000.

This figure is known as the random match probability (RMP). Since it is computed using the product rule for multiplying probabilities, it assumes that the patterns found in two distinct sites are independent. Is this assumption justified? Personally, I find this a particularly worrying assumption, and it very definitely is an assumption, but genetics is not my area of expertise, and (unlike the California Supreme Court) I do not feel comfortable stepping into the specialties of other professionals. Overall those specialists seem reasonably confident in the independence assumption. In any event, the courts regularly accept the independence assumption, and my present focus lies elsewhere, so for the purpose of this essay, I’ll simply accept it too.

Using DNA profiling

Here is one way that DNA profiling is often used in the criminal justice system. The authorities investigating a crime obtain evidence that points to a particular individual as the criminal, but fails to identify the suspect with sufficient certainty to obtain a conviction. If the suspect’s DNA profile is in the CODIS database, or else a sample is taken and a profile prepared, it may be compared with a profile taken from a sample collected at the crime scene. If the two profiles agree on all thirteen loci, then for all practical—and all legal—purposes, the suspect is assumed to have been identified with certainty. The random match probability (one in ten trillion) provides an estimate of the likelihood that the two profiles came from different individuals.

Of course, all that a DNA match does is identify—within a certain degree of confidence—an individual whose DNA profile was that same as that of a sample (or samples) found at the crime scene. In of itself, it does not imply that the individual committed the crime. There could be any number of ways for a person’s DNA to end up at a crime scene. (If your spouse or close friend were murdered, very likely some of your DNA would be found on the victim’s body or clothing. It does not follow automatically that you are the killer.) Other evidence is required to determine guilt of the crime in question.

As to the degree of confidence that can be vested in the identification of an individual by means of a DNA profile match obtained in the above manner, the issues to be considered are:

The likelihood of errors in collecting (and labeling) the two samples and determining the associated DNA profiles
The likelihood that the profile match is purely coincidental.

A likelihood of one in ten trillion attached to the second of these two possibilities (such as is given by the RMP for a 13-loci match) would clearly imply that the former possibility is far more likely, since hardly any human procedure can claim a one in ten trillion fallibility rate. Put differently, if there is no reason to doubt the accuracy of the sample collections procedures and the laboratory analyses, the DNA profile identification could surely be viewed with considerable confidence.

[I have already expressed my doubt regarding the use of the RMP to obtain a reliable indicator of an accidental match, computed as it is on the basis of our current scientific understanding of ggenetics. The RMP calculation does, after all, require mathematical independence of the loci—an extremely demanding condition—in order to be able to apply the product rule. I’d feel a lot more confident if there were some empirical data to buttress the accepted assumption. What empirical data there is seems if anything to support my doubt. A recent analysis of the Arizona convicted offender data base (a database that uses the 13 CODIS loci) revealed that among the approximately 65,000 entries listed there were 144 individuals whose DNA profiles match at 9 loci (including one match between individuals of different races, one Caucasion, the other African American), another few who match at 10 loci, one pair that match at 11, and one pair that match at 12. The 11 and 12 loci matches were siblings, hence not random. But matches on 9 or 10 loci among a database as small as 65,000 entries cast considerable doubt in my mind on figures such as the oft-cited “one in ten trillion” for a match that extends to just 3 or 4 additional loci. But again, this is off my current target.]

Of course, the a one-in-a-trillion likelihood figure is massive overkill. Absent any confounding factors, a figure of one in a million or one in ten million (say) would surely be enough to determine identity with virtual certainty.

Hence, all of the above cautions notwithstanding, it seems reasonable to assume that (blood relatives aside) a 13-loci match can be taken as definitive identification—provided that, and this is absolutely critical to the calculation and use of the RMP, the match is arrived at by comparing a profile from a sample from the crime scene with a profile taken from a sample from a suspect who has already been identified by means other than his or her DNA profile. But this is not what happened in the case that led to the recent decision by the California Supreme Court. The case before them involved a so-called “cold hit identification.”

Cold Hit searches

Increasingly, when criminal investigation authorities find themselves with crime scene DNA evidence but no suspects, they resort to using the DNA profile as a tool to identify a possible culprit, by searching DNA profile databases of previous offenders (such as the CODIS database) to see if a match can be found. A “cold hit” identification is one that results from such a search. A match obtained in this way would be a “cold hit” because, prior to the match, the individual concerned was not a suspect.

As in the case where DNA profiling is used to provide identification of an individual who was already a suspect, the principal question that has to be (or at least should be) asked after a cold hit search has led to a match (a “hit”) is: Does the match indicate that the profile in the database belongs to the same person whose sample formed the basis of the search, or is the match purely coincidental? At this point, the waters rapidly become very murky.

To illustrate the problems inherent in the Cold Hit procedure, consider the following analogy. A typical state lottery will have a probability of winning a major jackpot around 1 in 35,000,000. To any single individual, buying a ticket is clearly a waste of time. Those odds are effectively nil. But suppose that each week, at least 35,000,000 people actually do buy a ticket. (This is a realistic example.) Then every one to three weeks, on average, someone will win. The news reporters will go out and interview that lucky person. What is special about that person? Absolutely nothing. The only thing you can say about that individual is that he or she is the one who had the winning numbers. You can make absolutely no other conclusion. The 1 in 35,000,000 odds tell you nothing about any other feature of that person. The fact that there is a winner reflects the fact that 35,000,000 people bought a ticket – and nothing else.

Compare this to a reporter who hears about a person with a reputation of being unusually lucky, goes along with them as they buy their ticket, and sits alongside them as they watch the lottery result announced on TV. Lo and behold, that person wins. What would you conclude? Most likely, that there has been a swindle. With odds of 1 in 35,000,000, it’s impossible to conclude anything else in this situation.

In the first case, the long odds tell you nothing about the winning person, other than that they won. In the second case, the long odds tell you a lot.

To my mind, a Cold Hit measured by RMP is like the first case. All it tells you is that there is a DNA profile match. It does not, in of itself, tell you anything else, and certainly not that that person is guilty of the crime.

On the other hand, if an individual is identified as a crime suspect by means other than a DNA match, then a subsequent DNA match is like the second case. It tells you a lot. Indeed, assuming the initial identification had a rational, relevant basis (like a reputation for being lucky in the lottery case), the long RMP odds against a match could be taken as conclusive. But as with the lottery example, in order for the long odds to have (any) weight, the initial identification has to be before the DNA comparison is run (or at least demonstrably independent thereof). Do the DNA comparison first, and those impressive sounding long odds may be totally meaningless, simply reflecting the size of the relevant population, just as in the lottery case.

It has to be admitted that not everyone agrees with the above analogy—at least, they do not agree with the conclusions regarding the inapplicability of the RMP in the case of a cold hit match. In particular, the FBI has argued repeatedly that the RMP remains the only statistic that needs to be presented in court to provide a metric for the efficacy of a DNA cold hit match.

Unfortunately, attempts to resolve the issue by obtaining expert opinion have so far served only to muddy the waters still further.

The NRC reports

In 1989, the FBI urged the National Research Council to carry out a study of the matter. The NRC formed the Committee on DNA Technology in Forensic Science, which issued its report in 1992. Titled DNA Technology in Forensic Science, and published by the National Academy Press, the report is often referred to as “NRC I”. The committee’s main recommendation regarding the cold hit process is given on page 124 of the report:

“The distinction between finding a match between an evidence sample and a suspect sample and finding a match between an evidence sample and one of many entries in a DNA profile databank is important. The chance of finding a match in the second case is considerably higher. … The initial match should be used as probable cause to obtain a blood sample from the suspect, but only the statistical frequency associated with the additional loci should be presented at trial (to prevent the selection bias that is inherent in searching a databank).”

In part because of the controversy the NRC I report generated among scientists regarding the methodology proposed, and in part because courts were observed to misinterpret or misapply some of the statements in the report, in 1993, Judge William Sessions, then the Director of the FBI, asked the NRC to carry out a follow-up study. A second committee was assembled, and it issued its report in 1996. Often referred to as “NRC II”, the second report, The Evaluation of Forensic DNA Evidence, was published by the National Academy Press in 1996.

The NRC II committee’s main recommendation regarding cold hit probabilities is:

“Recommendation 5.1. When the suspect is found by a search of DNA databases, the random-match probability should be multiplied by N, the number of persons in the database.”

The statistic NRC II recommends using is generally referred to as the “database match probability”, DMP. This is an unfortunate choice of name, since the DMP is not a probability—although in all actual instances it is a number between 0 and 1, and it does (in my view as well as that of the NRC II committee) provide a good indication of the likelihood of getting an accidental match when a cold hit search is carried out. (The intuition is fairly clear. In a search for a match in a database of N entries, there are N chances of finding such a match.) For a true probability measure, if an event has probability 1, then it is certain to happen. However, consider a hypothetical case where a DNA database of 1,000,000 entries is searched for a profile having a RMP of 1/1,000,000. In that case, the DMP is

1,000,000 x 1/1,000,000 = 1

However, in this case the probability that the search will result in a match is not 1 but approximately 0.6312.

The committee’s explanation for recommending the use of the DMP to provide a scientific measure of the accuracy of a cold hit match reads as follows:

“A special circumstance arises when the suspect is identified not by an eyewitness or by circumstantial evidence but rather by a search through a large DNA database. If the only reason that the person becomes a suspect is that his DNA profile turned up in a database, the calculations must be modified. There are several approaches, of which we discuss two. The first, advocated by the 1992 NRC report, is to base probability calculations solely on loci not used in the search. That is a sound procedure, but it wastes information, and if too many loci are used for iidentification of the suspect, not enough might be left for an adequate subsequent analysis. … A second procedure is to apply a simple correction: Multiply the match probability by the size of the database searched. This is the procedure we recommend.” [p.32].

This is essentially the same logic as I presented for my analogy with the state lottery.

The controversy

Since two reports by committees of acknowledged experts in DNA profiling technology and statistical analysis, with each report commissioned by the FBI, came out strongly against the admissibility of the RMP, one might have imagined that would be the end of the matter, and that judges in a cold hit trial would rule in favor of admitting either the RMP for loci not used in the initial identification (à la NRC I) or else (à la NRC II) the DMP but not the RMP calculated on the full match.

However, not all statisticians agreed with the conclusions of the second NRC committee. Most notably, Dr. Peter Donnelly, Professor of Statistical Science at the University of Oxford, took a view diametrically opposed to that of NRC II. In an affidavit to the Court of the District of Columbia, in connection with a cold hit case (the Jenkins case), titled “DNA Evidence after a database hit” and dated October 3, 2004, Donnelly observed that during the preparation of the NRC II report, he had substantive discussions about the issues with four members of the committee whom he knew professionally, and went on to say:

“I had argued, and have subsequently argued, that after a database search, the DNA evidence … is somewhat stronger than in the setting in which the suspect is identified by non-DNA evidence and subsequently found to match the profile of the crime sample. … I disagree fundamentally with the position of NRC II. Where they argue that the DNA evidence becomes less incriminating as the size of the database increases, I (and others) have argued that in fact the DNA evidence becomes stronger. … The effect of the DNA evidence after a database search is two-fold: (i) the individual on trial has a profile which matches that of the crime sample, and (ii) every other person in the database has been eliminated as a possible perpetrator because their DNA profile differs from that of the crime sample. It is the second effect, of ruling out others, which makes the DNA evidence stronger after a database search…”

Donnelly advocated using a Bayesian analysis to determine the probability of a random match, which method he outlined in a paper co-written with David Balding in 1996, titled “Evaluating DNA Profile Evidence When the Suspect is Identified Through a Database Search” (J. Forensic Science 603) and again in a subsequent article co-written with Richard Friedman: “DNA Database Searches And The Legal Consumption Of Scientific Evidence”, Michigan Law Review, 00262234, Feb99, Vol. 97, Issue 4.

The statistic generated by the Donnelly/Balding method is generally close to the RMP, although it results from a very different calculation.

The Donnelly/Balding method was considered by NRC II and expressly rejected. (Readers knowledgable in probability theory will recognize at once that this is yet another manifestation of the ongoing debate between frequentist and Bayesian approaches to probability calculations.)

We thus have a fascinating situation: two groups of highly qualified experts in statistical reasoning, each proposing a different way to calculate the likelihood that a cold hit search will identify an innocent person, and each claiming that its method is correct and the other is dead wrong.

Scarcely any wonder then that the courts have become confused as to what number or numbers should be presented in court as evidence.

Personally, I (together with the collective opinion of the NRC II committee) find it hard to accept Donnelly’s argument, but his view does seem to establish quite clearly that the relevant scientific community (in this case statisticians) have not yet reached consensus on how best to compute the reliability metric for a cold hit.

As I understand it (as a non-lawyer), the accepted procedure for the courts to follow when there is no consensus regarding a scientific procedure is to rule inadmissible the introduction as evidence of results obtained by the disputed procedure. In this case, that would, I believe, make it very difficult to provide the RMP as the sole numerical indicator of the reliability of a DNA profile match obtained from a cold hit search, a state of affairs that the FBI, for one, appears to wish not to happen.

The question then is, what should the courts do? My personal view, as a mathematician, is that they should adopt one of the approaches recommended by the NRC, preferably NRC I (which is free of controversy), taking advantage of much improved DNA testing technology to extend the match process to more than 13 loci, a move that would more than compensate for the increase in the accidental match probability, however it is calculated, that results from a cold hit search.

What the courts should definitely not do, in my opinion (and let me stress that what you are reading is, as always in “Devlin’s Angle”, an opinion), is simply take it upon itself to decide, as a matter of law rather than scientific accuracy, which calculation should be used. That is not how the courts normally act in matters of scientific evidence, and in my view it is not how they should act here.

Yet this is exactly what the California Supreme Court has just done with its recent ruling. (The decision went 4 to 2 with one justice recusing himself. The court did not give the reasoning behind their decision.)

Two test cases

There are, to my knowledge, two cases currently before the California courts where there is dispute as to the admissibility of cold hit calculations, one of which led directly to the recent decision.

In one, People of the State of California versus Christopher Goree, the Los Angeles District Attorney, in his submission to the Los Angeles Superior Court dated 5/19/06, opposed the defendant’s motion to exclude DNA cold hit statistics resulting from a method currently in dispute, stating “. . .any argument regarding the relevance in a ‘cold hit case’ of a rarity/random match probability statistics is a legal argument, not a [. . .] scientific argument.”

Statisticians reading this may be shocked, but the DA meant what he said. Later in his motion, he argues: “Whether evidence has less probative value or more probative value is a legal evaluation, not a scientific one. Nothing prevents scientists from debating the issue, but its evaluation and resolution is reserved for the judiciary alone.”

While the first sentence in the above claim may well be correct from a legal standpoint, think very carefully about what is implied by the second sentence. We are, after all, talking here not about opinions, but what number, as a matter of actual fact, most accurately measures the mathematical likelihood of a false conviction. The fact that at present different groups of statisticians do not agree on the answer does not make this any less a matter of actual fact. It just means that the relevant professional community have not yet reached consensus on what that actual fact is.

This kind of thing is hardly unknown in science. Physicists are currently in disagreement as to whether string theory correctly describes the universe we live in. But should that too be a matter for the courts to resolve?

Yes, of course the courts are where decisions must be made as to what evidence may or may not be admitted. But when that evidence is a result of the application of science, they should do so in an informed way, upon the advice of the appropriate scientists. In that case of cold hit DNA cases, that means professional statisticians. If the statisticians agree on a number or numbers that describe a certain situation, the court must, if it decides such numbers are relevant, use that number or numbers – and definitely no others. If the statisticians express disagreement, the court would be wise to act on the assumption that either view may be correct. (Correct here does not mean which calculation is correct as a calculation. In the present cold hit controversy, no one argues that any particular calculation is incorrect. Rather, the “correctness” in dispute is which calculation (and hence the result of that calculation) best describes the actual situation before the court.)

The LA District Attorney goes on to say: “Defendant then postulates that when a single suspect is identified in a DNA database search, the significance of a subsequent one-to-one DNA profile comparison between the suspect and the perpetrator should not be described using the rarity/ransom match probability in the general population. He is wrong, however. [ . . . ] The exact means by which the suspect was initially identified are irrelevant.”

I know of no statistician, be he or she frequentist or Bayesian, who would agree to that last claim. Still, the DA is trying to secure a conviction. It is not his job to be faithful to science, rather to make the best case he can. What I find far more worrying are the decisions being made by the courts. For their job, after all, is to get at the truth.

In the second case I shall discuss, The People versus Michael Johnson, the Court of Appeal of the State of California Fifth Appellate District issued an opinion on May 25 of this year, in which they state: “In our view, the means by which a particular person comes to be suspected of a crime – the reason law enforcement’s investigation focuses on him – is irrelevant to the issue to be decided at trial, i.e., that person’s guilt or innocence.”

The court continues a short while later: ” . . . the fact that here, the genetic profile from the evidence sample (the perpetrator’s profile) matched the profile of someone in a database of criminal offenders, does not affect the strength of the evidence against appellant. [ . . . ] The fact appellant was first identified as a possible suspect based on a database search simply does not matter.”

Oh dear, oh dear, oh dear.

Again, I urge you to play out the above line of reasoning with my lottery example. Every week, millions and millions of lottery entrants are reminded of the huge difference between “the probability that someone will win” and “the probability that YOU will win.”

Subsequent to the court’s opinion on the Johnson case, I was one or several scientists who wrote an Amicus Brief to the California Supreme Court requesting that in cold hit cases as in other cases involving scientific issues, the courts should seek expert opinion from, in this case, statisticians.

[Incidentally, my only involvement in the general issue of probability calculations in DNA cold hit cases is that of a citizen concerned that justice be properly done, and a mathematician who believes I have a duty to ensure that the professional opinion of mathematicians should be taken into account when it is relevant. I have no connection with any case currently before the courts, and know nothing about any of them other than is available in public documents. I have no personal interested vested in whether the court accepts or denies a brief to which I am a cosignator.]

In our brief, we state:

By way of background, we make clear that we are scholars and scientists, not attorneys. Our professional interest is in the proper understanding of the role that science in general, and statistics in particular, can and should play in legal cases involving forensic DNA evidence. Assuming that criminal trials are a search for the truth, evidence presented before juries should be accurate. Forensic DNA evidence is grounded in statistical expressions that measure the likelihood of coincidence. Statisticians and other professional scientists with an interest in, and knowledge about, statistics and genetics are uniquely empowered to advise how to derive those statistical expressions. Science matters, and court decisions that treat statistical questions such as how to express match evidence in DNA database match cases as purely legal ones are, respectfully, irresponsible.”

By denying the petition for review in the Johnson case of which our brief was part, the California Supreme Court has ruled that, for now at least, it is for the courts to decide which statistical calculations to accept and which to keep out in cold hit cases. That strikes me as a scandalous afront to all professional statisticians, both those who regularly testify for the prosecutions and those who testify for the defendants in DNA profile cases.

Given the system of checks and balances in our legal system, I am hopeful that in due course the matter will be resolved correctly. In the meantime, I fear that the very DNA profiling procedure that has been used so successfully to overturn many previous false convictions (as well as put behind bars individuals I for one am glad are no longer roaming the streets), will, in the case of cold hit cases as currently being adjudicated, lead to another collection of wrongful convictions that later courts will have to undo.

Devlin’s Angle is updated at the beginning of each month.

OCTOBER 2006

Damned lies

Earlier this year, I gave an evening adult education course at Stanford. As you might expect, given our location in the heart of Silicon Valley, most of my 30 or so students had scientific or engineering degrees, many of them masters and PhDs, and their occupations were primarily engineers in the high tech industry, teachers, college instructors, and retirees from those professions. All in all, a numerate bunch, with many years of experience working in scientific and technical fields.

My topic for one class was the use of DNA profiling in law enforcement and criminal court cases. I explained to the class how the accuracy of DNA profiling as a means to identify people (usually crime suspects, who as a result of the identification become criminal defendants) depends crucially on a key statistic: the probability that a DNA profile match between (say) a defendant and a DNA sample taken from a crime scene was a result of an accidental match, rather than because the crime-scene sample came from the defendant. I then displayed on the screen a probability figure that prosecutors typically give in court:

1/15,000,000,000,000,000

or 1 in 15 quadrillion.

The class spontaneously erupted in laughter. Not just one or two students, but, as far as I could tell, all of them. For what this class of 30 or so experienced and numerically sophisticated scientists, technologists, engineers, and others realized at once was that such a figure is total nonsense. Nothing in life ever comes remotely close to such a degree of accuracy. In most professions where numerical precision is important, including laboratory science, 1 in 10,000 is often difficult to achieve.

I told the class that I was not trying to pull a fast one on them, and that I had read sworn testimonies to courts from scientists for the prosecution in serious criminal cases who insisted that such figures were both accurate and reliable. In the class discussion that followed, the general consensus seemed to be that anyone who makes such a statement in court is either numerically naive or else is deliberately trying to deceive a (possibly numerically unsophisticated) judge and jury.

Most regular readers will by now have a pretty good idea where a figure such as 1 in 15 quadrillion will have come from, and what it actually represents.

(Readers who saw last month’s column will also have realized that I am returning to the same topic I discussed then, namely DNA profiling. To avoid repetition, I will assume from here on that anyone reading this column has (recently) read last month’s offering, and I will assume familiarity with everything I discussed there.)

A DNA profile is essentially a read-out of an individual’s genetic material taken on a number of distinct loci, loci chosen because scientists believe that they exhibit considerable variation among the population. The variation at a chosen locus will typically be such that the probability of two randomly chosen individuals having the same read-out at that locus is 1-in-ten or less.

If the read-outs at different loci are independent (in the usual sense of probability theory), then you can employ the product rule to compute the probability that two randomly selected individuals have profiles that match on a given set of loci, say 5 loci, 10 loci, or 13 loci, the number of loci that is currently used by the FBI in their CODIS database of 3,000,000 or so profiles from convicted individuals.

Taking the 1/10 figure I used above as an example for the probability of a random match at a single locus, using the product rule gives a figure of

1 in 10,000,000,000,000

or 1 in 10 trillion for the probability of a match on 13 loci, a figure which, my conservative 1-in-10 example statistic notwithstanding, is still laughably well beyond the accuracy of human science and technology.

As often happens when the computation of probabilities is concerned, such unsophisticated use of the product rule rapidly takes theory well beyond the bounds of reality. I would not state such a ludicrous figure in a court of law, and nor, I am fairly sure, would any of my Stanford adult education class. And personally, as a mathematician, I find it a disgraceful state of affairs that the courts allow it. They may as well admit alchemy and astrology.

A figure such as 1 in ten trillion is so far off the reliability scale of science and technology that it says nothing about the likelihood that an innocent individual is in court accused of a crime. It answers one and one question only. Namely, the theoretical mathematical question, “If the probability of a single event is 1/10, and you run 13 independent trials, what is the probability that the event occurs in all 13 trials?”

So what figure should be presented in court? Actually, let me rehprase that. After my previous column appeared, I received a number of emails from lawyers, and some of them supported the view of the Supreme Court of California that the courts themselves should decide that matter – a state of affairs that I would be happy to concur with if they would seek the advice of professional statisticians in doing so, something that at present they seem reluctant to do. So, I’ll rephrase my question as, what figure should be presented in court if the aim is to provide the judge and jury with the best numerical measure of the actual probability that the defendant’s DNA profile match is accidental?

As I explained last month, that is a difficult question to answer, and the answer you get depends in significant part on how the defendant was first identified as a suspect. But my focus this month is not on the initial identification procedure, but on another matter that worries me, which I merely touched upon in passing last month. To whit:

Since naive application of the product rule leads to mumbo jumbo answers, just how do you calculate the probability of a random match on a specified set of loci?

Not by mathematics, or at least not by mathematics alone as is presently the case, that’s for sure. (I believe that one of the duties of a professional mathematician is to stand up and say when our powerful toolbox is not appropriate, and this in my view is one of those moments.)

If mathematics were to be used to compute a meaningful and reliable random match probability, then the first thing that would need to be done is to look very, very, very closely at that assumption of independence across the loci.

As far as I can tell (and remember that this is way outside my domain of expertise), very little is known about this. This is particularly worrying because, given the way the product rule works (and now I’m back in my domain), in particular the speed with which it starts to produce absurdly large answers, in order to compute a reliable profile match probability starting with match probabilities at individual loci, you would need extremely accurate (I would guess unachievably accurate) numerical information on the degrees of dependence.

So what should be done? To me, the answer is obvious. Instead of using mathematics, determine the various random match probabilities empirically.

As far as I am aware, to date there has been only one attempt to do this, and the results obtained were both startling and worrying. A study of the Arizona CODIS database carried out in 2005 showed that approximately 1 in every 228 profiles in the database matched another profile in the database at nine or more loci, that approximately 1 in every 1,489 profiles matched at 10 loci, 1 in 16,374 profiles matched at 11 loci, and 1 in 32,747 matched at 12 loci.

How big a population does it take to produce so many matches that appear to contradict so dramatically the astronomical, theoretical figures given by the naive application of the product rule? The Arizona database contained at the time a mere 65,493 entries. Scary isn’t it?

It is not much of a leap to estimate that the FBI’s national CODIS database of 3,000,000 entries will contain not just one but several pairs that match on all 13 loci, contrary (and how!) to the prediction made by proponents of the currently much touted RMP that you can expect a single match only when you have on the order of 15 quadrillion profiles.

Of course, to produce reliable data that will serve the cause of justice, such a study would have to be done with care. For example, it would be important to eliminate (or at least flag) when the same individual has two or more profiles in the same database, listed under multiple identities – something that one can imagine happening in a database of convicted criminals. It would also be important to flag close relatives, who have a greatly increased likelihood of sharing large sections of DNA. When that is done, it may turn out that, even when excised of those ludicrously astronomical numbers, DNA profiling as currently practiced remains a highly accurate means of identification with low probability of leading to a false conviction. (I sure hope so.)

But, given the extremely high stakes, and the amount of court time currently taken up arguing about numbers that scientists can (and should) determine accurately, once and for all, it seems to me that such a study needs to be carried out as a matter of some urgency.

With 3 million entries, the FBI CODIS database would seem to be easily large enough to yield statistically reliable results. In fact, given that any competent computer science undergraduate could probably write a program to perform such a study in rather less than a single afternoon, with the results available after a few minutes (seconds?) of computing time, I am amazed that this has not been done already.

FOOTNOTE: By the way, some of the correspondence I received after last month’s column seemed (I’m being generous with this wording) to suggest that my goal was to help dangerous criminals escape conviction and continue to do harm to innocent citizens. I find it impossible to get inside the mind of a citizen of a country based on what is to my mind the most impressive founding documents the world has ever seen (I refer to the Declaration of Independence, the US Constitution, and the Bill of Rights) who reads my words as anything but a sincere plea that we adhere to the principles set out in those documents. Consequently, I have no idea what I could say that would convince such a person otherwise.

Devlin’s Angle is updated at the beginning of each month.

NOVEMBER 2006

Will the real continuous function please stand up?

This column first appeared in May 2000. I am repeating it because I think the points raised are worth bringing up again.

What exactly is a continuous function? Here is a typical explanation taken from a university textbook (G. F. Simmons, Calculus with Analytic Geometry, McGraw-Hill, 1985):

In everyday speech, a ‘continuous’ process is one that proceeds without gaps of interruptions or sudden changes. Roughly speaking, a function y = f(x) is continuous if it displays similar behavior, that is, if a small change in x produces a small change in the corresponding value f(x).

As the author observes, this description is “rather loose and intuitive, and intended more to explain than to define.” He goes on to provide a “more rigorous, formal definition,” which I summarize as:

A function f is continuous at a number a if the following three conditions are satisfied:

1. f is defined on an open interval containing a.

2. f(x) tends to a limit as x tends to a.

3. That limit is equal to f(a).

To make this precise, we need to define the notion of a limit:

If a function f(x) is defined on an open interval containing a, except possibly at a itself, we say that f tends to a limit L as x tends to a, where L is a real number, if, for any \epsilon > 0, there is a \delta > 0 such that:

if 0 < |x – a| < \delta, then |f(x) – L| < \epsilon

With limits defined in this way, the resulting definition of a continuous function is known as the Cauchy-Weierstrass definition, after the two nineteenth century mathematicians who developed it. The definition forms the bedrock of modern real analysis and any standard “rigorous” treatment of calculus. As a result, it is the gateway through which all students must pass in order to enter those domains. But how many of us manage to pass through that gateway without considerable effort? Certainly, I did not, and neither has any of my students in twenty-five years of university mathematics teaching. Why is there so much difficulty in understanding this definition? Admittedly the logical structure of the definition is somewhat intricate. But it’s not that complicated. Most of us can handle a complicated definition provided we understand what that definition is trying to say. Thus, it seems likely that something else is going on to cause so much difficulty, something to do with what the definition means. But what, exactly?

Let’s start with the intuitive idea of continuity that we started out with, the idea of a function that has no gaps, interruptions, or sudden changes. This is essentially the conception Newton and Leibniz worked with. So too did Euler, who wrote of “a curve described by freely leading the hand.” Notice that this conception of continuity is fundamentally dynamic. Either we think of the curve as being drawn in a continuous (sic) fashion, or else we view the curve as already drawn and imagine what it is like to travel along it. This means that our mental conception has the following features:

1. The continuous function is formed by motion, which takes place over time.

2. The function has directionality.

3. The continuity arises from the motion.

4. The motion results in a static line with no gaps or jumps.

5. The static line has no directionality.

Aspects of this dynamic view are still present when we start to develop a more formal definition: we speak about the values f(x) approaching the value f(a) as x approaches a. The mental picture here is one of preserving closeness near a point.

Notice that the formal definition of a limit implicitly assumes that the real line is continuous (i.e., gapless, or a continuum). For, if it were not, then talk about x approaching a would not capture the conception we need. In this conception, a line or a continuum is a fundamental object in its own right. Points are simply locations on lines.

When we formulate the final Cauchy-Weierstrass definition, however, by making precise the notion of a limit, we abandon the dynamic view, based on the idea of a gapless real continuum, and replace it by an entirely static conception that speaks about the existence of real numbers having certain properties. The conception of a line that underlies this definition is that a line is a set of points. The points are now the fundamental objects, not the line. This, of course, is a highly abstract conception of a line that was only introduced in the late nineteenth century, and then only in response to difficulties encountered dealing with some pathological examples of functions.

When you think about it, that’s quite a major shift in conceptual model, from the highly natural and intuitive idea of motion (in time) along a continuum to a contrived statement about the existence of numbers, based on the highly artificial view of a line as being a set of points. When we (i.e., mathematics instructors) introduce our students to the “formal” definition of continuity, we are not, as we claim, making a loose, intuitive notion more formal and rigorous. Rather, we are changing the conception of continuity in almost every respect. No wonder our students don’t see how the formal definition captures their intuitions. It doesn’t. It attempts to replace their intuitive picture with something quite different.

Perhaps our students would have less trouble trying to understand the Cauchy-Weierstrass definition if we told them in advance that it was not a formalization of their intuitive conception — that the mathematician’s formal notion of a continuous function is in fact something quite different from the intuitive picture. Indeed, that might help. But if we are getting into the business of open disclosure, we had better go the whole way and point out that the new definition does not explicitly capture continuity at all. That famous—indeed, infamous—epsilon-delta statement that causes everyone so much trouble does not eliminate (all) the vagueness inherent in the intuitive notion of continuity. Indeed, it doesn’t address continuity at all. Rather, it simply formalizes the notion of “correspondingly” in the relation “correspondingly close.” In fact, the Cauchy-Weierstrass definition only manages to provide a definition of continuity of a function by assuming continuity of the real line!

It is perhaps worth mentioning, if only because some students may have come to terms with the idea that a line is a set of points, that in terms of that conception of a line — which is not something that someone or something can move along—the original, intuitive idea of continuity reduces simply to gaplessness. In short, however you approach it, the step from the intuitive notion of continuity to the formal, Cauchy-Weierstrass definition, involves a huge mental discontinuity.

NOTE: This article is based on the paper Embodied cognition as grounding for situatedness and context in mathematics education, by R. Nunez, L. Edwards, and J. Matos, Educational Studies in Mathematics 39 (1999), pp.45-65.

Devlin’s Angle is updated at the beginning of each month.

DECEMBER 2006

The biggest science breakthrough of the year

The image says it all. When SCIENCE magazine declares that the proof of a theorem in mathematics is the breakthrough of the year in all of science, you know that something special has occurred.

We’ve had a double wait for this breakthrough. Henri Poincare first formulated his now famous conjecture just over 100 years ago, in 1904, and despite several heroic attempts to prove it, the puzzle remained unsolved until late 2002 and through into 2003, when the somewhat reclusive Russian mathematician Grigori Perelman posted a series of three papers on the Internet that claimed to outline a proof of the Thurston Geometrization Conjecture, which was known to yield the Poincare Conjecture as a consequence.

That was the first wait. But another was in store. Such was the intricacy of Perelman’s argument, compounded by the highly compressed manner in which he presented it, that is took over three years of effort by various groups around the world before the consensus agreement came in: he had indeed proved the Poincare Conjecture. (The experts are still unsure about Perelman’s proof of the Geometrization Conjecture.)

What made it a major science story, I think, is only in part the magnitude of the advance within mathematics. Proofs of major theorems are often of interest to the entire scientific community, but they rarely earn the accolade of “the scientific breakthrough of the year.” (Off hand, no previous example comes to mind, but perhaps some readers have a better memory than I for that kind of thing.) I suspect that the editors of SCIENCE gave their vote to this particular theorem because it lies at the heart of the domain (if not the practice) of physics.

Of course, faced with having compared apples with oranges, the editors at SCIENCE did not disclose their criteria. But, in his editorial, editor-in-chief Donald Kennedy does say what appealed to him about the result: “The analysis [described in SCIENCE] struck me as a fascinating exploration, full of metaphors suggesting a multidisciplinary dimension in Perelman’s analysis. He first got interested in Ricci flow, a process by which topological regions of high curvature flow into regions of lower curvature. He also identified a quantity, which he called “entropy,” that increased during the flow, providing a gradient. Tight spots in spatial connections block the application of these rules to dimensions higher than two, so Perelman dealt with these through “surgical intervention.” This story is rich with borrowings: from fluid mechanics, thermodynamics, and even surgery! It’s hard to deal with a three-dimensional object in four-dimensional space. Perelman’s solution is a stunning triumph of intellect.”

Most of the techniques Kennedy alludes to were not developed until long after Poincare had died, but perhaps we should not be surprised that his conjecture required such a rich repertoire of physically-based techniques for its solution. For, although Poincare is generally thought of as one of the greatest mathematicians of all time, his interests were as much in physics as in mathematics, and he came within a whisker of formulating relativity theory before Einstein beat him to the punch. Although usually formulated as a pure mathematics problem about the classification of abstract manifolds, the Poincare conjecture is really about the structure of the space we live in, and the degree to which we humans, as prisoners within that space, unable to break free and observe it from the outside, may nevertheless determine some key features of its structure.

Poincare proposed a procedure which he believed would enable us to make such a determination. It is not a practical procedure, and was never intended to be viewed as such. Thanks to Perelman, we now know that Poincare’s proposed method is indeed sufficient to determine the structure of space from the inside—in theory. But viewed from the perspective of physics, it’s really an epistemological result, which tells us that the structure of space is in principal knowable, even though the procedure Poincare proposed is not a practical one.

To appreciate what Poincare proposed, consider the analogy of a two-dimensional ant living on a surface (actually, it lives in the surface). From the outside, looking down on the ant’s world, we see the creature’s universe as a surface. It could be (the surface of) a sphere, a torus (the surface of a ring donut), a two-holed torus, etc. From our viewpoint, we could see which it is. But would the ant living in the surface have any way of knowing the shape? For each of those possible shapes, the ant has exactly the same freedom of movement, forwards and backwards or left and right.

Poincare asked the analogous question of our 3-D universe. We can, at least in principle, travel forwards and backwards, left and right, up and down. But as with the ant, this freedom of movement does not tell us the shape. Since we can’t step outside our universe and look down on it, is there any way that we could determine the shape of our universe from the inside?

The Poincare conjecture says that the following procedure will do the trick. Imagine we set off on a long spaceship journey. (This is not how Poincare formulated the conjecture; he used the formal mathematical language of topology and geometry.) As we travel, we unreel a long string behind us. After journeying a long while, we decide it is time to head home—not necessarily the same way we went out. When we return to our starting point, we make a slipknot in our string and begin pulling the string through. One of two things can then happen. Either the noose eventually pulls down to a point or else it reaches a stage where, no matter how much we pull, it cannot shrink down any further.

Poincare’s conjecture is that if we can always shrink the loop to a point, then the space we live in is the 3D analog of the surface of a sphere; but if we can find a start/end point and a journey where the loop cannot be shrunk to a point, then our universe must have one or more “holes”, much like a torus. (Essentially, what is going on is that our string “snags” by going around such a hole.)

In the case of our two-dimensional ant, it is easy to prove that such a procedure does indeed enable the creature to determine from the inside whether its universe is like the surface of a sphere or whether there are holes. But until Perelman came along, nobody had proved the same technique would work for us in our three-dimensional universe and allow us in principle to tell from the inside what kind of universe we live in. We now know that we can. In fact, the more general Geometrization Conjecture that Perelman’s argument also established tells us we can in principle determine a great deal more about the shape of the universe.

As I mentioned already, although the Poincare conjecture is about a fundamental question of physics, it is essentially an epistemological matter. There is, as far as I know, no automatic consequence of the conjecture in terms of everyday physics. But the methods Perelman used to finally prove the conjecture seem likely to have major implications in physics. To push through his argument, Perelman had to develop powerful methods to handle singularities. And that may prove to be the start of a whole new chapter in mathematical physics. Stay tuned, scientists.

P.S. Discover magazine also listed the proof of the Poincare conjecture as one of the top 100 science stories of 2006, but they ranked it as number 8. Their story led off with a conjecture of its own: that the proof of the Poincare conjecture may turn out to be the number 1 math story of the entire 21st century. I definitely agree. But then, I would. I wrote the Discover story.

Devlin’s Angle is updated at the beginning of each month.